
Απάντηση
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![\displaystyle{ \frac{1}{2} \int_{- \infty}^{+ \infty} \frac{ \cos [ (n-1) x] - \cos [ (n+1) x ]}{x^2} \mathrm{d}x} \displaystyle{ \frac{1}{2} \int_{- \infty}^{+ \infty} \frac{ \cos [ (n-1) x] - \cos [ (n+1) x ]}{x^2} \mathrm{d}x}](/forum/ext/geomar/texintegr/latexrender/pictures/6dbccf37ddfe1a9b01c3007221929a9b.png)
 σε ημικύκλιο με κέντρο το
σε ημικύκλιο με κέντρο το  και στο θετικό φανταστικό ημιεπίπεδο. Στο
και στο θετικό φανταστικό ημιεπίπεδο. Στο  η συνάρτηση έχει απλό πόλο υπολοίπου
η συνάρτηση έχει απλό πόλο υπολοίπου  , οπότε το παρακάμπτουμε από τα αρνητικά φανταστικά μέρη. Το ολοκλήρωμα θα έχει τιμή
, οπότε το παρακάμπτουμε από τα αρνητικά φανταστικά μέρη. Το ολοκλήρωμα θα έχει τιμή  και θα εκφράζεται ως :
και θα εκφράζεται ως :
 ,
, 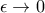 και πραγματικά μέρη καταλήγουμε σε
και πραγματικά μέρη καταλήγουμε σε ![\displaystyle{\int_{-\infty}^{+ \infty} \frac{\cos [(n-1) x] - \cos [(n+1) x]}{2x^2} \mathrm{d} x + \pi = 2 \pi} \displaystyle{\int_{-\infty}^{+ \infty} \frac{\cos [(n-1) x] - \cos [(n+1) x]}{2x^2} \mathrm{d} x + \pi = 2 \pi}](/forum/ext/geomar/texintegr/latexrender/pictures/edd6b6ee1da920f1363e639ae1875a3a.png) , οπότε
, οπότε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες