Ασκηση
Θέτουμε
 και
και ![f:[0, 1]\rightarrow R f:[0, 1]\rightarrow R](/forum/ext/geomar/texintegr/latexrender/pictures/8fe18f3495a18ec55862c14aad09a454.png) με f(0)=0,
με f(0)=0, 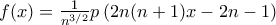 αν
αν  . Να αποδειχθούν τα ακόλουθα:
. Να αποδειχθούν τα ακόλουθα:α. Η f είναι παραγωγίσιμη.
β. Η f ' δεν είναι συνεχής.
γ. Το σύνολο τιμών της f' στο [0, δ] είναι το
 για τυχόν δ>0.
για τυχόν δ>0.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 και
και ![f:[0, 1]\rightarrow R f:[0, 1]\rightarrow R](/forum/ext/geomar/texintegr/latexrender/pictures/8fe18f3495a18ec55862c14aad09a454.png) με f(0)=0,
με f(0)=0, 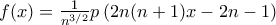 αν
αν  . Να αποδειχθούν τα ακόλουθα:
. Να αποδειχθούν τα ακόλουθα: για τυχόν δ>0.
για τυχόν δ>0.Ροδόλφε μπορείς να το κάνεις συγκεκριμένο ;
Εχει δίκιο ο Ροδόλφος.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΡΑΤΟΣ έγραψε: ↑Πέμ Οκτ 01, 2009 6:57 pmΚαλησπέρα στο φόρουμ
Ασκηση
Θέτουμεκαι
με f(0)=0,
αν
. Να αποδειχθούν τα ακόλουθα:
α. Η f είναι παραγωγίσιμη.
β. Η f ' δεν είναι συνεχής.
γ. Το σύνολο τιμών της f' στο [0, δ] είναι τογια τυχόν δ>0.
 στο
στο![[0,\delta ] [0,\delta ]](/forum/ext/geomar/texintegr/latexrender/pictures/d256d740c71ea29e6d365cad82be682b.png) είναι το
είναι το  για τυχόν
για τυχόν 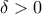
 ?
?Επειδή με βάση τον τύπο είναι
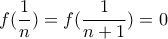

 είναι
είναι 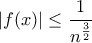
 .
.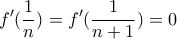
![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png)
 είναι
είναι 

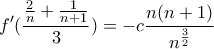

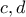 απόλυτες θετικές σταθερές.(βγαίνουν συγκεκριμένα νούμερα)
απόλυτες θετικές σταθερές.(βγαίνουν συγκεκριμένα νούμερα)Ακριβώς.
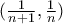
 .
. έχει παράγωγο στο
έχει παράγωγο στο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες