Όμορφο .. αλλά αρκετά ζόρικο γενικευμένο ολοκλήρωμα
Δημοσιεύτηκε: Σάβ Οκτ 10, 2009 10:53 pm
[color=brown]Όντως είναι [b]πανέμορφο[/b] ...[/color]
https://www.mathematica.gr/forum/
 .
. με
με  (Δ. Δασκαλόπουλος ΕΜΠ 3ος Τόμος, σελίδες 355-356)
(Δ. Δασκαλόπουλος ΕΜΠ 3ος Τόμος, σελίδες 355-356) τότε
τότε 

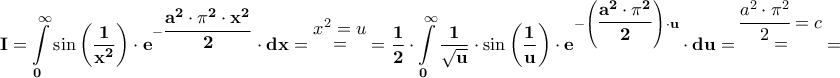

 με
με 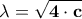 και
και 
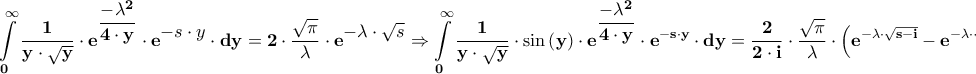
 θα έχουμε ότι
θα έχουμε ότι ![\displaystyle{\mathbf{\sqrt {s - i} = \sqrt[4]{{{s^2} + 1}} \cdot \left( {\cos \left( {\frac{\theta }{2}} \right) - i \cdot \sin \left( {\frac{\theta }{2}} \right)} \right) = \sqrt {\frac{{\sqrt {{s^2} + 1} + s}}{2}} - i \cdot \sqrt {\frac{{\sqrt {{s^2} + 1} - s}}{2}}} } \displaystyle{\mathbf{\sqrt {s - i} = \sqrt[4]{{{s^2} + 1}} \cdot \left( {\cos \left( {\frac{\theta }{2}} \right) - i \cdot \sin \left( {\frac{\theta }{2}} \right)} \right) = \sqrt {\frac{{\sqrt {{s^2} + 1} + s}}{2}} - i \cdot \sqrt {\frac{{\sqrt {{s^2} + 1} - s}}{2}}} }](/forum/ext/geomar/texintegr/latexrender/pictures/f326282345fcc1f10d37e930ffe57e41.png)



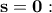



 και για a: ακέραιο έχουμε το ζητούμενο.
και για a: ακέραιο έχουμε το ζητούμενο.