Cesaro Stolz 0/0 ισχυρή μορφή

#1

Καλησπέρα. Έχει κανείς κάποια παραπομπή (με απόδειξη κατά προτίμηση) για την ακόλουθη ισχυρή μορφή του Cezaro Stolz;

Αν

1) $\displaystyle{\lim_{n\to+\infty}a_n=\lim_{n\to+\infty}b_n=0}$ ,

2) Η b_n

είναι γνησίως φθίνουσα,

3) $\displaystyle{\lim_{n\to+\infty}\frac{a_{n+1}-a_n}{b_{n+1}-b_n}=\ell\in\mathbb R\cup\{\pm\infty\}}$ ,

τότε $\displaystyle{\lim_{n\to+\infty}\frac{a_n}{b_n}=\ell}$ .

Αυτή την εκδοχή δεν την είχα υπόψη μου. Η πιο ισχυρή εκδοχή που είχα συναντήσει απαιτούσε και η a_n

να φθίνει στο

, μέχρι που είδα σε ένα άρθρο να χρησιμοποιούν την παραπάνω και βρήκα αυτό (σελ 10) αλλά τις παραπομπές που δίνει δεν τις βρίσκω στο δίκτυο..

#2

Αναστάση πρωτοείδα το θέμα στο βιβλίο:
Ilyin, Poznyak, Fundamentals of Mathematical Analysis, Part 1, Mir, 1982
όπου υπάρχει (σελίδα 86) η ακόλουθη εκδοχή που νομίζω ότι με μία μικρή τροποποίηση δίνει κάτι παραπάνω από αυτό που ζητάς:
Θεώρημα Stolz Έστω $\left\{ y_{n}\right\}$ μία απειριζόμενη αύξουσα ακολουθία και έστω ότι η ακολουθία $\left\{ \frac{x_{n}-x_{n-1}}{y_{n}-y_{n-1}}\right\}$ συγκλίνει στο

. Τότε και η ακολουθία $\left\{ \frac{x_{n}}{y_{n}}\right\}$ συγκλίνει και έχει όριο το

. Επομένως
$\lim\limits_{n\rightarrow +\infty }\frac{x_{n}}{y_{n}}=\lim\limits_{n\rightarrow +\infty }\frac{x_{n}-x_{n-1}}{y_{n}-y_{n-1}}$ .

Η απόδειξη πιάνει 3 1/2 σελίδες. Αν σε ενδιαφέρει μου λες.

Ίσως είναι χρήσιμα
α) το άρθρο της wikipedia:
https://en.wikipedia.org/wiki/Stolz%E2% ... ro_theorem
β) το άρθρο
A.G.Ramm, Discrete L'Hospital's rule
στο http://arxiv.org/abs/math/0504034

Μαυρογιάννης

#3

Νίκο καλησπέρα. Την εκδοχή που αναφέρεις την έχω υπόψη μου αλλά επειδή, για την περίπτωση 0/0, όποια εκδοχή έχω δει ζητάει αριθμητή και παρονομαστή να φθίνει στο 0, δεν σκέφτηκα ότι μπορεί η παραπάνω εκδοχή να τροποποιηθεί δίνοντας τη 0/0 με ασθενείς υποθέσεις (μόνο ο παρονομαστής να φθίνει στο 0). Δεν ξέρω αν η τροποποίηση που λες είναι άμεση. Δεν το έχω σκεφτεί. Θα το κοιτάξω.

#4

Κοτρώνης Αναστάσιος έγραψε:Καλησπέρα. Έχει κανείς κάποια παραπομπή (με απόδειξη κατά προτίμηση) για την ακόλουθη ισχυρή μορφή του Cezaro Stolz;

Αν

1) $\displaystyle{\lim_{n\to+\infty}a_n=\lim_{n\to+\infty}b_n=0}$ ,

2) Η είναι γνησίως φθίνουσα,

3) $\displaystyle{\lim_{n\to+\infty}\frac{a_{n+1}-a_n}{b_{n+1}-b_n}=\ell\in\mathbb R\cup\{\pm\infty\}}$ ,

τότε $\displaystyle{\lim_{n\to+\infty}\frac{a_n}{b_n}=\ell}$ .

Αυτή την εκδοχή δεν την είχα υπόψη μου. Η πιο ισχυρή εκδοχή που είχα συναντήσει απαιτούσε και η να φθίνει στο , μέχρι που είδα σε ένα άρθρο να χρησιμοποιούν την παραπάνω και βρήκα αυτό (σελ 10) αλλά τις παραπομπές που δίνει δεν τις βρίσκω στο δίκτυο..

Αναστάση,
όταν ξαναβρεθούμε να θυμηθούμε να σου φέρω το βιβλίο του Κώστα Μπροχούτα, Άλγεβρα.
Όταν έδινα για τη ΦΜΣ το 1977 ήταν το βιβλίο από το οποίο έμαθα ακολουθίες. Είναι καταπληκτικό. ΕΚεί θα δει κανένας πόσες σπουδαίες προτάσεις αποδεικνύονται με αυτή την εξαιρετική πρόταση.
Τώρα, για την απόδειξη, δε θυμάμαι που την έχω δει.Νομίζω ότι κάποια φορά είχα δει μία με τον κανόνα de L'Hospital.
Θα κοιτάξω και θα σου πω , αν βρώ κάτι άλλο.

***Α! Πήγα βιβλιοθήκη και είδα το βιβλίο. Έχει μέσα και την απόδειξη(με τον ορισμό του ορίου ακολουθίας), μια σελίδα και κάτι, αλλά κατανοητή.

Μπάμπης

Ilias_Zad · #5

Δεν ξέρω τι αποδείξεις έχουν μέσα τα παραπάνω βιβλία αλλά μπορούμε να το δούμε ως εξής:
Για

πραγματικό,
Έστω e>0

.

Tότε υπάρχει n_0

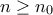τέτοιο ώστε για κάθε $n\geq n_0$ να ισχύει :

$l-e<\frac{a_n-a_{n-1}}{b_n-b_{n-1}}< l+e$ και άρα $(l+e )(b_n-b_{n-1})< a_n-a_{n-1} <(l-e)(b_n-b_{n-1})$ αν $n\geq n_0$ .

Αν τώρα παρόυμε ένα $m \geq n_0$ τότε για N >m

αθροίζοντας την τελευταία σχέση
για n=m+1,..,N

παίρνουμε ότι ισχύει (l+e)(b_N-b_m)<a_N-a_m<(l-e)(b_N-b_m)

.

Αυτή η σχέση όμως με

στο άπειρο δίνει $-(l+e)b_m \leq -a_m \leq-(l-e)b_m \rightarrow l-e \leq \frac{a_m}{b_m} \leq l+e$ , και άρα το ζητούμενο.

Για

άπειρο η αντιμετώπιση είναι όμοια με ένα σωστό πείραγμα στην πρώτη σχέση.

Cesaro Stolz 0/0 ισχυρή μορφή

Cesaro Stolz 0/0 ισχυρή μορφή

Re: Cesaro Stolz 0/0 ισχυρή μορφή

Re: Cesaro Stolz 0/0 ισχυρή μορφή

Re: Cesaro Stolz 0/0 ισχυρή μορφή

Re: Cesaro Stolz 0/0 ισχυρή μορφή

Μέλη σε σύνδεση