
όπου
 η σταθερά του Catalan http://mathworld.wolfram.com/CatalansConstant.html
η σταθερά του Catalan http://mathworld.wolfram.com/CatalansConstant.html Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

 η σταθερά του Catalan http://mathworld.wolfram.com/CatalansConstant.html
η σταθερά του Catalan http://mathworld.wolfram.com/CatalansConstant.html  τότε από το θεώρημα Beppo-Levi έχουμε
τότε από το θεώρημα Beppo-Levi έχουμε  .Επίσης έχουμε
.Επίσης έχουμε  .
. .Με μια απλή επαγωγή έχουμε ότι
.Με μια απλή επαγωγή έχουμε ότι  . Από εδώ εύκολα βρίσκουμε ότι
. Από εδώ εύκολα βρίσκουμε ότι  συνεπώς
συνεπώς  .
.
 .
. εύκολα προκύπτει ότι
εύκολα προκύπτει ότι  , άρα έχουμε ότι
, άρα έχουμε ότι  .
. .Άρα εύκολα βλέπουμε ότι
.Άρα εύκολα βλέπουμε ότι 
 ,
, . Tελικά έχουμε ότι
. Tελικά έχουμε ότι  .
. έχουμε ότι
έχουμε ότι  , και θέτοντας
, και θέτοντας  βρίκουμε ότι η
βρίκουμε ότι η  ικανοποιεί την διαφορική εξίσωση:
ικανοποιεί την διαφορική εξίσωση: 
 έχουμε ότι
έχουμε ότι  οπότε
οπότε  .
. συγκλίνει (επειδή το αρχικό ολοκλήρωμα υπάρχει) από το λήμμα του Abel ισχύει
συγκλίνει (επειδή το αρχικό ολοκλήρωμα υπάρχει) από το λήμμα του Abel ισχύει  συνεπώς
συνεπώς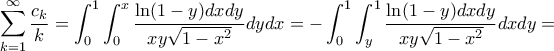
 .Θέτοντας
.Θέτοντας  βρίσκουμε
βρίσκουμε  και
και  ,
,
 .Άρα προκύπτει ότι
.Άρα προκύπτει ότι  .
. , επομένως
, επομένως  .
.Πολύ όμορφη η λύση σου Κώσταkwstas12345 έγραψε:Πολύ όμορφο θέμα. Θέτουμετότε από το θεώρημα Beppo-Levi έχουμε
...
 .. κι εγώ έτσι ξεκίνησα αλλά κόλλησα .. κι άλλαξα πλεύση ..
.. κι εγώ έτσι ξεκίνησα αλλά κόλλησα .. κι άλλαξα πλεύση ..
 , οπότε
, οπότε 


 viewtopic.php?f=9&t=12954&hilit=otto , οπότε
viewtopic.php?f=9&t=12954&hilit=otto , οπότε 

 http://mathworld.wolfram.com/CatalansConstant.html
http://mathworld.wolfram.com/CatalansConstant.html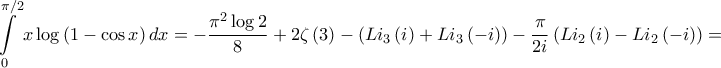

Μέλη σε αυτήν τη Δ. Συζήτηση: Mihalis_Lambrou και 6 επισκέπτες