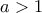 να αποδειχθούν τα :
να αποδειχθούν τα :  και
και 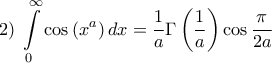 ,
, όπου
 η συνάρτηση Γάμμα του Euler http://mathworld.wolfram.com/GammaFunction.html
η συνάρτηση Γάμμα του Euler http://mathworld.wolfram.com/GammaFunction.html Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
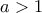 να αποδειχθούν τα :
να αποδειχθούν τα :  και
και 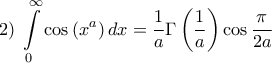 ,
,  η συνάρτηση Γάμμα του Euler http://mathworld.wolfram.com/GammaFunction.html
η συνάρτηση Γάμμα του Euler http://mathworld.wolfram.com/GammaFunction.html 
 .
.

 .
. στο οποίο επιτρέπεται η εναλλαγή και έπειτα αφήνουμε το
στο οποίο επιτρέπεται η εναλλαγή και έπειτα αφήνουμε το  να πάει στο άπειρο.Επίσης χρησιμοποιήθηκε η γνωστή ιδιότητα
να πάει στο άπειρο.Επίσης χρησιμοποιήθηκε η γνωστή ιδιότητα  .Tα ολοκληρώματα
.Tα ολοκληρώματα  υπολογίζονται εντελώς παρόμοια ξεκινώντας από τα ολοκληρώματα
υπολογίζονται εντελώς παρόμοια ξεκινώντας από τα ολοκληρώματα 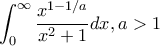 .
.
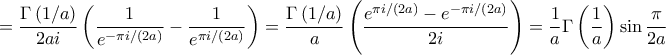
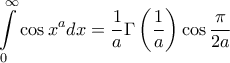 .
. εφαρμόζεται ο μετασχηματισμός Laplace με μιγαδική μεταβλητή μηδενικού πραγματικού μέρους (κριτήριο Cauchy).
εφαρμόζεται ο μετασχηματισμός Laplace με μιγαδική μεταβλητή μηδενικού πραγματικού μέρους (κριτήριο Cauchy).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες