Δινεται η συναρτηση
 τετοια ωστε, για καθε
τετοια ωστε, για καθε  , υπαρχουν τα πλευρικα ορια
, υπαρχουν τα πλευρικα ορια  και
και  με τιμες στο
με τιμες στο  .
.Να αποδειχθει οτι το πληθος των σημειων ασυνεχειας της
 ειναι το πολυ αριθμησιμο.
ειναι το πολυ αριθμησιμο.Δημητρης
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 τετοια ωστε, για καθε
τετοια ωστε, για καθε  , υπαρχουν τα πλευρικα ορια
, υπαρχουν τα πλευρικα ορια  και
και  με τιμες στο
με τιμες στο  .
. ειναι το πολυ αριθμησιμο.
ειναι το πολυ αριθμησιμο. και κάθε n, υπάρχει
και κάθε n, υπάρχει  ώστε για κάθε
ώστε για κάθε  έχουμε
έχουμε  και για κάθε
και για κάθε  έχουμε
έχουμε  . Τότε, για οποιοδήποτε
. Τότε, για οποιοδήποτε  με
με  έχουμε
έχουμε  .
. .
. . Όλα τα διαστήματα
. Όλα τα διαστήματα  έχουν ανά δύο κενή τομή. Από αυτό συμπεραίνω ότι το πλήθος των χ για το οποία
έχουν ανά δύο κενή τομή. Από αυτό συμπεραίνω ότι το πλήθος των χ για το οποία  είναι αριθημίσιμο. Άρα και το πλήθος των σημείων ασυνέχεις της f είναι αριθμήσιμο.
είναι αριθημίσιμο. Άρα και το πλήθος των σημείων ασυνέχεις της f είναι αριθμήσιμο. το συνολο των σημειων ασυνεχειας της
το συνολο των σημειων ασυνεχειας της  . Για τυχαιο
. Για τυχαιο  θετουμε
θετουμε 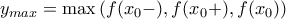 και
και  . Προφανως
. Προφανως  και μπορουμε να επιλεξουμε ρητο
και μπορουμε να επιλεξουμε ρητο 
 τετοιο ωστε, για καθε
τετοιο ωστε, για καθε  με
με  να ισχυει
να ισχυει  για καποιο θετικο
για καποιο θετικο  (ανεξαρτητο του
(ανεξαρτητο του  ). Επιλεγουμε ρητο
). Επιλεγουμε ρητο  και αντιστοιχιζουμε στο
και αντιστοιχιζουμε στο  το διατεταγμενο ζευγος
το διατεταγμενο ζευγος  .
. που αντιστοιχιζεται στο
που αντιστοιχιζεται στο  :
: , οποτε
, οποτε 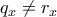 ,
,  , οποτε εκ κατασκευης
, οποτε εκ κατασκευης  .
. στο
στο  και κατα συνεπεια το
και κατα συνεπεια το  ειναι το πολυ αριθμησιμο.
ειναι το πολυ αριθμησιμο.Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 5 επισκέπτες