 . Να δείξετε ότι:
. Να δείξετε ότι:  όπου
όπου  είναι ο
είναι ο  -ιοστός αρμονικός όρος.
-ιοστός αρμονικός όρος.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 . Να δείξετε ότι:
. Να δείξετε ότι:  όπου
όπου  είναι ο
είναι ο  -ιοστός αρμονικός όρος.
-ιοστός αρμονικός όρος.
Τάσο τώρα το είδα. Γενικότερα ανΚοτρώνης Αναστάσιος έγραψε:Τόλη μήπως πρέπει να αναφέρεις τι είναι ο δεύτερος προσθετέος για κάποιον που δεν έχει ξαναδεί το συμβολισμό;
 τότε
τότε 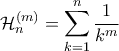 είναι ο
είναι ο  -ιοστός
-ιοστός  αρμονικός όρος. Οπότε στη περίπτωσή μας έχουμε
αρμονικός όρος. Οπότε στη περίπτωσή μας έχουμε 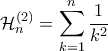 .
.


 διότι
διότι  Άλλος τρόπος;
Άλλος τρόπος;
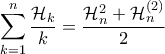 .
.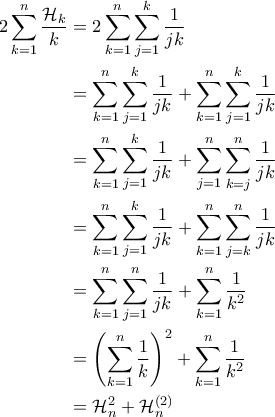


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 22 επισκέπτες