Να υπολογιστεί το όριο :

Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Απάντηση:

 στο
στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) και
και 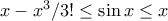 στο
στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) έχουμε
έχουμε  και
και  για
για 

 έως
έως  , παίρνοντας όριο και με χρήση του
, παίρνοντας όριο και με χρήση του  έχουμε από ισοσυγκλίνουσες
έχουμε από ισοσυγκλίνουσες  , από όπου το ζητούμενο.
, από όπου το ζητούμενο.ΘέτουμεTolaso J Kos έγραψε: ↑Δευ Μαρ 26, 2018 9:03 pmΓια όποιον δεν έχει να κάνει κάτι καλύτερο σήμερα βράδυ Δευτέρας .
Να υπολογιστεί το όριο :



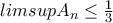 (0)
(0) (1)
(1)
 (2)
(2)

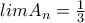
![S_n (f, [0,1]) S_n (f, [0,1])](/forum/ext/geomar/texintegr/latexrender/pictures/932b2f2d04f371beb21dfdbd096f5af5.png) το άθροισμα Riemann της
το άθροισμα Riemann της  στο
στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) με ομοιόμορφη διαμέριση
με ομοιόμορφη διαμέριση  στοιχείων και με ετικέτες το δεξί άκρο κάθε στοιχείου.
στοιχείων και με ετικέτες το δεξί άκρο κάθε στοιχείου. η οποία συγκλίνει ομοιόμορφα στο
η οποία συγκλίνει ομοιόμορφα στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) στην
στην  (π.χ. με κριτήριο ομοιομορφίας Cauchy).
(π.χ. με κριτήριο ομοιομορφίας Cauchy).![\displaystyle \lim_{n \to \infty} \left( S_n (f_n, [0,1]) - S_n (x^2, [0,1]) \right) = 0 \displaystyle \lim_{n \to \infty} \left( S_n (f_n, [0,1]) - S_n (x^2, [0,1]) \right) = 0](/forum/ext/geomar/texintegr/latexrender/pictures/6c0f32392e702ca65d6ce41e96d016f1.png) . Επίσης ισχύει
. Επίσης ισχύει ![\displaystyle \lim_{n \to \infty} S_n (x^2, [0,1]) = \int_0^1 x^2 \mathrm{d}x \displaystyle \lim_{n \to \infty} S_n (x^2, [0,1]) = \int_0^1 x^2 \mathrm{d}x](/forum/ext/geomar/texintegr/latexrender/pictures/ddbf7820bca051f42de89428c5b35866.png) .
. ![\displaystyle \lim_{n \to \infty} S_n (f_n, [0,1]) = \int_0^1 x^2 \mathrm{d}x = \frac{1}{3} \displaystyle \lim_{n \to \infty} S_n (f_n, [0,1]) = \int_0^1 x^2 \mathrm{d}x = \frac{1}{3}](/forum/ext/geomar/texintegr/latexrender/pictures/0a36a6f3702731383dcaa87eb75a38db.png) , που είναι το ζητούμενο.
, που είναι το ζητούμενο.Και αλλιώς: Από την σειρά Taylor της
 είναι
είναι 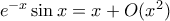 . Για
. Για  (όπου
(όπου  ) συμπεραίνουμε ότι
) συμπεραίνουμε ότι  .
.  έως
έως  το δοθέν άθροισμα ισούται
το δοθέν άθροισμα ισούται 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες