![f:[{0,1}]\longrightarrow\mathbb{R} f:[{0,1}]\longrightarrow\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/fa9401bcfae43df43f8e9fcaedb5f4f3.png) μία συνάρτηση δύο φορές παραγωγίσημη
μία συνάρτηση δύο φορές παραγωγίσημη με φραγμένη δεύτερη παράγωγο
Να αποδειχθεί ότι, για κάθε
 , υπάρχει
, υπάρχει 
ώστε

Από την οποία τετριμμένα παίρνουμε
Αν

τότε

Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![f:[{0,1}]\longrightarrow\mathbb{R} f:[{0,1}]\longrightarrow\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/fa9401bcfae43df43f8e9fcaedb5f4f3.png) μία συνάρτηση δύο φορές παραγωγίσημη
μία συνάρτηση δύο φορές παραγωγίσημη  , υπάρχει
, υπάρχει 



 καθώς και
καθώς και 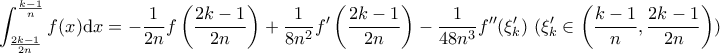 . Αφαιρώντας κατά μέλη παίρνουμε
. Αφαιρώντας κατά μέλη παίρνουμε  . Προσθέτοντας από
. Προσθέτοντας από  ως
ως  παίρνουμε
παίρνουμε .
. . Έτσι,
. Έτσι, 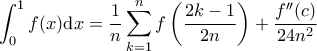 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες