 , να εξετασθεί η σύγκλιση της σειράς
, να εξετασθεί η σύγκλιση της σειράς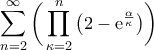
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 , να εξετασθεί η σύγκλιση της σειράς
, να εξετασθεί η σύγκλιση της σειράς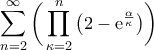

Η σειρά συγκλίνει αν και μόνο αν




 .
.





 οπότε είναι φραγμένη.
οπότε είναι φραγμένη.


 .
. βλέπε
βλέπε Εναλλακτικά, έχουμε ότι:


 και διαφορετικά αποκλίνει.
και διαφορετικά αποκλίνει. όπως δείχνεται και παρακάτω στο ποστ
όπως δείχνεται και παρακάτω στο ποστΚαλησπέρα Σωτήρη.
 το κριτήριο του Raabe δεν δίνει τίποτα. Ετσι πρέπει να λερώσεις τα χέρια σου για
το κριτήριο του Raabe δεν δίνει τίποτα. Ετσι πρέπει να λερώσεις τα χέρια σου για  .
. η
η  μηδενίζεται από κάπου και πέρα.
μηδενίζεται από κάπου και πέρα. , τότε
, τότε 

 για
για  η σειρά
η σειρά  συγκλίνει και
συγκλίνει και  για
για  η σειρά
η σειρά  απειρίζεται.
απειρίζεται. για
για  το κριτήριο Raabe δεν δίνει συμπέρασμα. Για την σύγκλιση της σειράς
το κριτήριο Raabe δεν δίνει συμπέρασμα. Για την σύγκλιση της σειράς  :
: , ισχύει
, ισχύει
 και επειδή,
και επειδή,  , από την
, από την  και το κριτήριο σύγκρισης, έπεται ότι
και το κριτήριο σύγκρισης, έπεται ότι  . Άρα και
. Άρα και  .
.


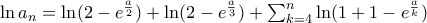





Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες