
όπου
 η συνάρτηση Möbius. Θα ήθελα να δω, αν υπάρχει, και κάποια "συμμαζεμένη" απόδειξη, τόσο για την σύγκλιση, όσο και για το αποτέλεσμα.
η συνάρτηση Möbius. Θα ήθελα να δω, αν υπάρχει, και κάποια "συμμαζεμένη" απόδειξη, τόσο για την σύγκλιση, όσο και για το αποτέλεσμα.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

 η συνάρτηση Möbius. Θα ήθελα να δω, αν υπάρχει, και κάποια "συμμαζεμένη" απόδειξη, τόσο για την σύγκλιση, όσο και για το αποτέλεσμα.
η συνάρτηση Möbius. Θα ήθελα να δω, αν υπάρχει, και κάποια "συμμαζεμένη" απόδειξη, τόσο για την σύγκλιση, όσο και για το αποτέλεσμα.

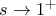 βγάζουμε ότι
βγάζουμε ότι
 . Αν μπορούσαμε να περάσουμε το όριο μέσα στη σειρά τότε τελειώσαμε. Το θέμα εδώ είναι ότι το να δείξει κάποιος ότι
. Αν μπορούσαμε να περάσουμε το όριο μέσα στη σειρά τότε τελειώσαμε. Το θέμα εδώ είναι ότι το να δείξει κάποιος ότι
 είναι ισοδύναμη με το θεώρημα των πρώτων αριθμών.
είναι ισοδύναμη με το θεώρημα των πρώτων αριθμών.


Εξαιρετικά ενδιαφέρον.Tolaso J Kos έγραψε: ↑Πέμ Αύγ 23, 2018 9:54 pm...Σημείωση 1: Μπορεί κάποιος να δείξει με στοιχειώδη μέσα ότι η απόδειξη της σειράςείναι ισοδύναμη με το θεώρημα των πρώτων αριθμών....
 έχει νόημα (ισχύει), για κάθε
έχει νόημα (ισχύει), για κάθε  με
με  .
.
Μάλιστα,
 αποκλίνει. Ίσως να ήταν ενδιαφέρον να τη δούμε σε ξεχωριστό topic.
αποκλίνει. Ίσως να ήταν ενδιαφέρον να τη δούμε σε ξεχωριστό topic.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες