Όριο γινομένου

Tolaso J Kos · #1

Ας δειχθεί ότι:

$\displaystyle{\lim_{n \rightarrow +\infty} \prod_{k=1}^{n} \left ( 1 + \frac{k^r}{n^{r+1}} \right ) = e^{1/(r+1)}}$

sot arm · #2

Tolaso J Kos έγραψε: ↑
Σάβ Νοέμ 24, 2018 11:29 am
Ας δειχθεί ότι:

$\displaystyle{\lim_{n \rightarrow +\infty} \prod_{k=1}^{n} \left ( 1 + \frac{k^r}{n^{r+1}} \right ) = e^{1/(r+1)}}$

Καλησπέρα Τόλη, βασιζόμενοι στο ανάπτυγμα Taylor της ln(1+x)

και το γεγονός ότι: $\displaystyle{\frac{k}{n} \in [0,1]}$ έχουμε:

$\displaystyle{x-x^{2}\leq ln(1+x)\leq x}$

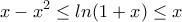
(Για τα x που μας ενδιαφέρουν)

Βάζουμε $x=(\frac{k}{n})^{r}\frac{1}{n}$ και αθροίζουμε απο 1 έως n έπεται:

$\displaystyle{\frac{1}{n}\sum_{k=1}^{n}(\frac{k}{n})^{r}-\frac{1}{n}(\frac{1}{n}\sum_{k=1}^{n}(\frac{k}{n})^{2r})\leq ln(\prod_{k=1}^{n} \left ( 1 + \frac{k^r}{n^{r+1}} \right ))\leq \frac{1}{n}\sum_{k=1}^{n}(\frac{k}{n})^{r}}$

Τέλος, παίρνοντας το όριο και αναγνωρίζοντας τα αθροίσματα Riemmann δεξιά και αριστερά στην ανισότητα έπεται:
$\displaystyle{ln( \prod_{k=1}^{\infty} \left ( 1 + \frac{k^r}{n^{r+1}} \right )\rightarrow \int_{0}^{1}x^{r}dx=\frac{1}{r+1}}$

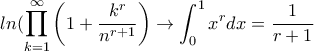
και το ζητούμενο έπεται.

Υ.Γ. γιατί μπορεί να μην είναι προφανές:
$\displaystyle{\frac{1}{n}(\frac{1}{n}\sum_{k=1}^{n}(\frac{k}{n})^{2r})\rightarrow 0\cdot\int_{0}^{1}x^{2r}dx=0}$

Όριο γινομένου

Όριο γινομένου

Re: Όριο γινομένου

Μέλη σε σύνδεση