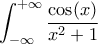
Σχόλιο: γιατί όπως είπε και ένας σοφός, αν δεν πεταχτεί ένα
 ή ένα
ή ένα  από εκεί που δεν το περιμένεις τι γούστο θα χε η ανάλυση.
από εκεί που δεν το περιμένεις τι γούστο θα χε η ανάλυση.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
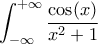
 ή ένα
ή ένα  από εκεί που δεν το περιμένεις τι γούστο θα χε η ανάλυση.
από εκεί που δεν το περιμένεις τι γούστο θα χε η ανάλυση.Με Μιγαδική ολοκλήρωση, λίγο γενικότερα
 . (Θα έλεγα ότι το ολοκλήρωμα αυτό ή παρεμφερή, υπάρχουν εν γένει σε βιβλία Μιγαδικής Ανάλυσης, αλλά άντε ψάξε το. Χάριν αυτονομίας, γράφω τα παρακάτω)
. (Θα έλεγα ότι το ολοκλήρωμα αυτό ή παρεμφερή, υπάρχουν εν γένει σε βιβλία Μιγαδικής Ανάλυσης, αλλά άντε ψάξε το. Χάριν αυτονομίας, γράφω τα παρακάτω) στο άνω ημικύκλιο με άκρα διαμέτρου τα
στο άνω ημικύκλιο με άκρα διαμέτρου τα  έχουμε ότι έχουμε απλό πόλο στο
έχουμε ότι έχουμε απλό πόλο στο  με κατάλοιπο
με κατάλοιπο  . Άρα
. Άρα 
 είναι
είναι 
 από Λήμμα Jordan. Ακριβέστερα
από Λήμμα Jordan. Ακριβέστερα  .
.Πολύ ωραία κύριε Λάμπρου, έχω και μία αντιμετώπιση με καθαρά χρήση πραγματικής, αποφεύγω να την γράψω για την ώρα μήπως θέλει να δοκιμάσει κάποιος άλλος.Mihalis_Lambrou έγραψε: ↑Σάβ Δεκ 01, 2018 1:34 pmΜε Μιγαδική ολοκλήρωση, λίγο γενικότερα. (Θα έλεγα ότι το ολοκλήρωμα αυτό ή παρεμφερή, υπάρχουν εν γένει σε βιβλία Μιγαδικής Ανάλυσης, αλλά άντε ψάξε το. Χάριν αυτονομίας, γράφω τα παρακάτω)
Πράγματι με ολοκλήρωση τηςστο άνω ημικύκλιο με άκρα διαμέτρου τα
έχουμε ότι έχουμε απλό πόλο στο
με κατάλοιπο
. Άρα
Όμως λόγω περιττότητας τηςείναι
Το άλλο ολοκλήρωμα τείνει στοαπό Λήμμα Jordan. Ακριβέστερα
.
Και λοιπά.
Θεωρούμε τη συνάρτηση
 . Παραγωγίζουμε ως προς
. Παραγωγίζουμε ως προς  οπότε,
οπότε,

 . Λαμβάνοντας υπόψιν ότι
. Λαμβάνοντας υπόψιν ότι 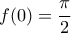 και
και 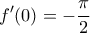 έχουμε ότι
έχουμε ότι  καθώς η γενική λύση της διαφορικής είναι γνωστό ότι είναι
καθώς η γενική λύση της διαφορικής είναι γνωστό ότι είναι 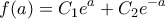 . Το αποτέλεσμα έπεται ότι το ολοκλήρωμα ισούται με:
. Το αποτέλεσμα έπεται ότι το ολοκλήρωμα ισούται με:

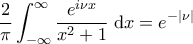

Πολύ ωραία Τόλη, είναι αυτό που έκανα και εγώ για την επίλυση, υπάρχει μία ακόμα λύση με μετασχημό Laplace αλλά δεν την ανεβάζω γιατί δεν έχω πλήρω εξοικείωση με τις τεχνικές λεπτομέριες.Tolaso J Kos έγραψε: ↑Σάβ Δεκ 01, 2018 2:05 pmΘεωρούμε τη συνάρτηση. Παραγωγίζουμε ως προς
οπότε,

Συνεπώς

Ξανά παραγωγίζοντας βγάζουμε. Λαμβάνοντας υπόψιν ότι
και
έχουμε ότι
καθώς η γενική λύση της διαφορικής είναι γνωστό ότι είναι
. Το αποτέλεσμα έπεται ότι το ολοκλήρωμα ισούται με:

Ωραία. Ας δούμε μία λύση με Laplace. Για ευκολία θα κάνω το ισοδύναμο
 .
.

 , όπως θέλαμε.
, όπως θέλαμε. (όπου
(όπου  σταθερό), που είναι απλό αλλά και έτοιμο από πίνακες. Επίσης, στο τελευταίο βήμα με τον αντίστροφο μετασχηματισμό, πάλι δουλεύουμε (όπως πάντα σε αυτές τις περιπτώσεις) από πίνακες. Συμβαίνει άλλωστε ο αντίστροφος της
σταθερό), που είναι απλό αλλά και έτοιμο από πίνακες. Επίσης, στο τελευταίο βήμα με τον αντίστροφο μετασχηματισμό, πάλι δουλεύουμε (όπως πάντα σε αυτές τις περιπτώσεις) από πίνακες. Συμβαίνει άλλωστε ο αντίστροφος της  να είναι το απλούστερο δυνατό παράδειγμα, και το μαθαίνει κανείς ως το πρώτο-πρώτο παράδειγμα σε αυτή την θεωρία. Τέλος, το προτελευταίο "=" είναι βέβαια με arctan).
να είναι το απλούστερο δυνατό παράδειγμα, και το μαθαίνει κανείς ως το πρώτο-πρώτο παράδειγμα σε αυτή την θεωρία. Τέλος, το προτελευταίο "=" είναι βέβαια με arctan).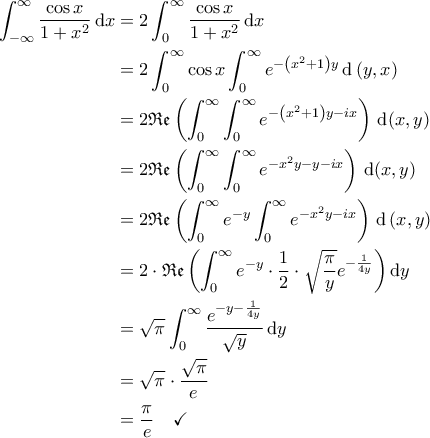
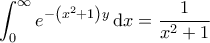
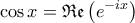
 ( γνωστός τύπος )
( γνωστός τύπος ) ( αφήνεται στον αναγνώστη )
( αφήνεται στον αναγνώστη )
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες