
Από σημερινή εξέταση Απ. ΙΙΙ κάπου στην Ελλάδα!
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος


 . Η συνάρτηση
. Η συνάρτηση  είναι συνεχής στο συμπαγές
είναι συνεχής στο συμπαγές  . Επομένως παίρνει μέγιστη και ελάχιστη τιμή στο
. Επομένως παίρνει μέγιστη και ελάχιστη τιμή στο  .
.  :
: 
 παρουσιάζει τοπικό (αλλά όχι ολικό) μέγιστο στα σημεία του συνόλου
παρουσιάζει τοπικό (αλλά όχι ολικό) μέγιστο στα σημεία του συνόλου  και τοπικό (αλλά όχι ολικό) ελάχιστο στα σημεία του συνόλου
και τοπικό (αλλά όχι ολικό) ελάχιστο στα σημεία του συνόλου  .
.  :
: ,
,  και
και 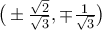 .
. ,
,  και
και  .
.  ισχύει
ισχύει 
 είναι η
είναι η  , την οποία παίρνει σε κάθε σημείο του συνόλου
, την οποία παίρνει σε κάθε σημείο του συνόλου  , και η ελάχιστη τιμή της
, και η ελάχιστη τιμή της  είναι η
είναι η  , την οποία παίρνει σε κάθε σημείο του συνόλου
, την οποία παίρνει σε κάθε σημείο του συνόλου  .
.
Μια ερώτηση. Αυτό το κάπου ποιο είναι ;Tolaso J Kos έγραψε: ↑Τετ Φεβ 13, 2019 9:19 pmΝα βρείτε και να χαρακτηρίσετε τα ακρότατα της συνάρτησης:

Από σημερινή εξέταση Απ. ΙΙΙ κάπου στην Ελλάδα!
![\frac{x^{2}}{2}+\frac{x^{2}}{2}+y^{2}\geq 3\sqrt[3]{(\frac{x^{4}y^{2}}{4})} \frac{x^{2}}{2}+\frac{x^{2}}{2}+y^{2}\geq 3\sqrt[3]{(\frac{x^{4}y^{2}}{4})}](/forum/ext/geomar/texintegr/latexrender/pictures/8fe10ce493364fa1c30a423cad2d6d5c.png)

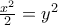
Και εγώ την ίδια απορία έχω γιατί δεν μπορούμε να πούμε από ποιο πανεπιστήμιο και τμήμα είναι τα θέματα; Το θεωρούμε μη σημαντικό; καλύπτονται από κάποιο copyright ανωνυμίας;
Δεν νομίζω ότι υπάρχει πρόβλημα δικαιωμάτων. Το θέμα είναι από την προχθεσινή εξέταση Απ. Λογισμού ΙΙΙ στο Μαθηματικό Ιωαννίνων.

 έχουμε
έχουμε 
 στο
στο ![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) μεγιστοποιείται/ελαχιστοποιείται είτε όταν
μεγιστοποιείται/ελαχιστοποιείται είτε όταν  είτε στα άκρα. Οπότε παίρνουμε
είτε στα άκρα. Οπότε παίρνουμε  και τα υπόλοιπα τώρα είναι απλά.
και τα υπόλοιπα τώρα είναι απλά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες