https://www.mathematica.gr/forum/viewto ... =9&t=64234
Αν

και
 .
.Το
 λέγεται σημείο συμπύκνωσης του
λέγεται σημείο συμπύκνωσης του  αν για κάθε
αν για κάθε 
το σύνολο
 είναι υπεραριθμήσιμο.
είναι υπεραριθμήσιμο.Να δειχθεί ότι :
Αν
 είναι υπεραριθμήσιμο σύνολο
είναι υπεραριθμήσιμο σύνολο τότε το σύνολο των σημείων του που δεν είναι σημεία συμπύκνωσης
είναι το πολύ αριθμήσιμο.
Βοηθάει το εξής:
το παραπάνω ισχύει σε οποιονδήποτε
 αριθμήσιμο μετρικό χώρο.
αριθμήσιμο μετρικό χώρο.(δηλαδή έχει αριθμήσιμη βάση περιοχών)

 τα
τα 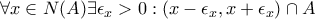 αριθμήσιμο.
αριθμήσιμο. του
του  και
και  .
. του
του 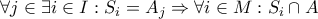 αριθμήσιμο.
αριθμήσιμο.
 που είναι
που είναι 
 υπεραριθμήσιμο.
υπεραριθμήσιμο. με
με 

 το σύνολο των σημείων του
το σύνολο των σημείων του  που δεν είναι σημεία συμπύκνωσης.
που δεν είναι σημεία συμπύκνωσης. υπάρχει ανοικτό
υπάρχει ανοικτό 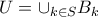


 το πολύ αριθμήσιμο
το πολύ αριθμήσιμο

