Ημιτονικό ... όριο

Tolaso J Kos · #1

Τι μπορείτε να πείτε για το όριο:

$\displaystyle{\ell = \lim_{n \rightarrow +\infty} \frac{1}{n \sin n}}$

#2

Tolaso J Kos έγραψε: ↑
Τετ Απρ 17, 2019 12:46 am
Τι μπορείτε να πείτε για το όριο:

$\displaystyle{\ell = \lim_{n \rightarrow +\infty} \frac{1}{n \sin n}}$

Θα δείξουμε ότι το όριο δεν υπάρχει.

Έστω ότι το όριο υπάρχει και έστω

η τιμή του. Από την πυκνότητα της $\cos n$ , υπάρχει υπακολουθία n_k

τέτοια ώστε $\cos n_k \to 1$ . Είναι τότε

$\displaystyle{L = \lim \frac {1}{2n_k \sin (2n_k)}= \lim \frac {1}{4n_k \sin (n_k)\cos (n_k)}= \lim \frac {1}{4n_k \sin (n_k)}\lim \frac {1}{\cos (n_k)}= \frac {L}{4}\cdot 1}$

και άρα L=0

. Θα δείξουμε τώρα ότι αποκλείεται να είναι

.

Από Θεώρημα Διοφαντικής προσέγγισης άρρητων (Dirichlet) υπάρχει ακολουθία $\displaystyle{\left ( \frac {p_n}{q_n}\right ) }$ με $\displaystyle{\left |2\pi - \frac {p_n}{q_n}\right | \le \frac {1}{q_n^2} }$ και άρα $\displaystyle{\left |2q_n\pi - p_n\right | \le \frac {1}{q_n} }$ . Έπεται

$\displaystyle{\left | \frac{1}{p_n \sin p_n} \right | = \left | \frac{1}{p_n \sin (2q_n\pi - p_n)} \right |\ge \left | \frac{1}{p_n (2q_n\pi - p_n)} \right |\ge \frac{q_n}{p_n }\to \frac {1}{2\pi} >0}$ . Άτοπο.

Τελικά, το όριο δεν υπάρχει.

stranger · #3

Mihalis_Lambrou έγραψε: ↑
Σάβ Απρ 20, 2019 7:39 pm

Tolaso J Kos έγραψε: ↑
Τετ Απρ 17, 2019 12:46 am
Τι μπορείτε να πείτε για το όριο:

$\displaystyle{\ell = \lim_{n \rightarrow +\infty} \frac{1}{n \sin n}}$
Θα δείξουμε ότι το όριο δεν υπάρχει.

Έστω ότι το όριο υπάρχει και έστω η τιμή του. Από την πυκνότητα της $\cos n$ , υπάρχει υπακολουθία 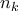τέτοια ώστε $\cos n_k \to 1$ . Είναι τότε

$\displaystyle{L = \lim \frac {1}{2n_k \sin (2n_k)}= \lim \frac {1}{4n_k \sin (n_k)\cos (n_k)}= \lim \frac {1}{4n_k \sin (n_k)}\lim \frac {1}{\cos (n_k)}= \frac {L}{4}\cdot 1}$

και άρα . Θα δείξουμε τώρα ότι αποκλείεται να είναι .

Από Θεώρημα Διοφαντικής προσέγγισης άρρητων (Dirichlet) υπάρχει ακολουθία $\displaystyle{\left ( \frac {p_n}{q_n}\right ) }$ με $\displaystyle{\left |2\pi - \frac {p_n}{q_n}\right | \le \frac {1}{q_n^2} }$ και άρα $\displaystyle{\left |2q_n\pi - p_n\right | \le \frac {1}{q_n} }$ . Έπεται

$\displaystyle{\left | \frac{1}{p_n \sin p_n} \right | = \left | \frac{1}{p_n \sin (2q_n\pi - p_n)} \right |\ge \left | \frac{1}{p_n (2q_n\pi - p_n)} \right |\ge \frac{q_n}{p_n }\to \frac {1}{2\pi} >0}$ . Άτοπο.

Τελικά, το όριο δεν υπάρχει.

Μου άρεσε που χρησιμοποιήθηκε το θεώρημα προσέγγισης αρρήτων του Dirichlet.
Αυτά είναι βαριά εργαλεία.

Ημιτονικό ... όριο

Ημιτονικό ... όριο

Re: Ημιτονικό ... όριο

Re: Ημιτονικό ... όριο

Μέλη σε σύνδεση