Να υπολογισθεί το όριο της ακολουθίας
![\displaystyle{ \sqrt [n]{\left (c+ \frac {1}{n} \right ) \left (c+ \frac {2}{n} \right ) \left (c+ \frac {3}{n} \right )\cdot ... \, \cdot \left (c+ \frac {n}{n} \right )}} \displaystyle{ \sqrt [n]{\left (c+ \frac {1}{n} \right ) \left (c+ \frac {2}{n} \right ) \left (c+ \frac {3}{n} \right )\cdot ... \, \cdot \left (c+ \frac {n}{n} \right )}}](/forum/ext/geomar/texintegr/latexrender/pictures/aab0956c89849904721e7209e53d01e9.png) , όπου
, όπου  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![\displaystyle{ \sqrt [n]{\left (c+ \frac {1}{n} \right ) \left (c+ \frac {2}{n} \right ) \left (c+ \frac {3}{n} \right )\cdot ... \, \cdot \left (c+ \frac {n}{n} \right )}} \displaystyle{ \sqrt [n]{\left (c+ \frac {1}{n} \right ) \left (c+ \frac {2}{n} \right ) \left (c+ \frac {3}{n} \right )\cdot ... \, \cdot \left (c+ \frac {n}{n} \right )}}](/forum/ext/geomar/texintegr/latexrender/pictures/aab0956c89849904721e7209e53d01e9.png) , όπου
, όπου  .
.ΈστωMihalis_Lambrou έγραψε: ↑Σάβ Δεκ 28, 2019 10:32 pmΆσκηση 9
Να υπολογισθεί το όριο της ακολουθίας
, όπου
.
![a_n=\displaystyle{ \sqrt [n]{\left (c+ \frac {1}{n} \right ) \left (c+ \frac {2}{n} \right ) \left (c+ \frac {3}{n} \right )\cdot ... \, \cdot \left (c+ \frac {n}{n} \right )}}. a_n=\displaystyle{ \sqrt [n]{\left (c+ \frac {1}{n} \right ) \left (c+ \frac {2}{n} \right ) \left (c+ \frac {3}{n} \right )\cdot ... \, \cdot \left (c+ \frac {n}{n} \right )}}.](/forum/ext/geomar/texintegr/latexrender/pictures/1be36b784cdf852b80500cfe08b5fca3.png)
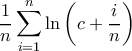 το οποίο είναι ίσο με
το οποίο είναι ίσο με![\displaystyle \int_{0}^{1}\ln\left ( c+x \right )dx= \int_{c}^{c+1}\ln xdx=\left [ x\ln x-x \right ]_{c}^{c+1}= \displaystyle \int_{0}^{1}\ln\left ( c+x \right )dx= \int_{c}^{c+1}\ln xdx=\left [ x\ln x-x \right ]_{c}^{c+1}=](/forum/ext/geomar/texintegr/latexrender/pictures/675d21d0d540730958818a23093bb540.png)
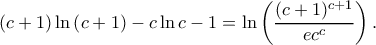


 θετικός πραγματικός μεγαλύτερος της μονάδας.
θετικός πραγματικός μεγαλύτερος της μονάδας.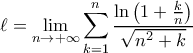

Έχουμε


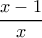 είναι γνησίως αύξουσα και ότι
είναι γνησίως αύξουσα και ότι 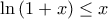


 και τις τελευταίες παίρνουμε
και τις τελευταίες παίρνουμε





Βγάζοντας το
 από τη ρίζα θέλουμε να υπολογίσουμε το όριο της ακολουθίας
από τη ρίζα θέλουμε να υπολογίσουμε το όριο της ακολουθίας 
![\displaystyle \int_{0}^{1}\dfrac{1}{\sqrt{4-x^2}}dx=\left [ \arcsin \left ( \dfrac{x}{2} \right ) \right ]_{0}^{1}=\dfrac{\pi }{6}. \displaystyle \int_{0}^{1}\dfrac{1}{\sqrt{4-x^2}}dx=\left [ \arcsin \left ( \dfrac{x}{2} \right ) \right ]_{0}^{1}=\dfrac{\pi }{6}.](/forum/ext/geomar/texintegr/latexrender/pictures/3e24e18657e4f41f7d646b0aeb352160.png)
 )
)
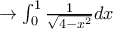 και στο ολοκλήρωμα
και στο ολοκλήρωμα  με
με 
 άρα
άρα 
H παράσταση είναι ανάμεσα στις
 και
και  (άμεσο). Και ο δύο τείνουν στο
(άμεσο). Και ο δύο τείνουν στο 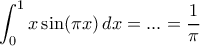 (στάνταρ κατά παράγοντες). Και λοιπά.
(στάνταρ κατά παράγοντες). Και λοιπά.Εφαρμόζοντας ίδιο σκεπτικό με την Άσκηση 11:Λάμπρος Κατσάπας έγραψε: ↑Σάβ Ιαν 04, 2020 11:43 pmΆσκηση 10
Να υπολογιστεί το όριο
όπουθετικός πραγματικός μεγαλύτερος της μονάδας.


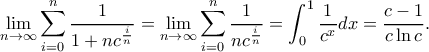
Λάμπρος Κατσάπας έγραψε: ↑Παρ Ιαν 10, 2020 8:53 pmΆσκηση 10
Να υπολογιστεί το όριο
όπουθετικός πραγματικός μεγαλύτερος της μονάδας.
 και
και  .
. . Και λοιπά.
. Και λοιπά.Πιο απλά.
 και στο
και στο 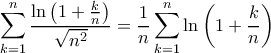 .
.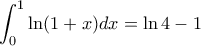 . Και λοιπά.
. Και λοιπά. συνεχής και μονότονη συνάρτηση και έστω
συνεχής και μονότονη συνάρτηση και έστω  ακολουθία θετικών όρων με
ακολουθία θετικών όρων με 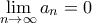 . Τότε
. Τότε
![\displaystyle{ \dfrac {1}{n} \sqrt [n] {\left(n+ d \right ) \left (n+ 2d \right ) \left (n+ 3d \right )\cdot ... \, \cdot \left (n+ nd)} \right )}} \displaystyle{ \dfrac {1}{n} \sqrt [n] {\left(n+ d \right ) \left (n+ 2d \right ) \left (n+ 3d \right )\cdot ... \, \cdot \left (n+ nd)} \right )}}](/forum/ext/geomar/texintegr/latexrender/pictures/abfb9d29380d73033d11f42f745d228b.png) , όπου
, όπου 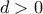 .
. . Η ομοιότητα εκτός από οπτική, είναι βαθύτερη).
. Η ομοιότητα εκτός από οπτική, είναι βαθύτερη).

Σίγουρα; Όπως είναι αποκλίνει στο άπειρο αφού
 και το
και το 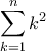 είναι της τάξης (σταθερά επί)
είναι της τάξης (σταθερά επί) 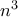 .
. . Σωστά;
. Σωστά;
Απάντηση:
 . Το κάνω κάπως σχολαστικά για όφελος των φοιτητών.
. Το κάνω κάπως σχολαστικά για όφελος των φοιτητών.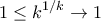 έχουμε
έχουμε  .
. . Επιλέγουμε
. Επιλέγουμε  τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε  είναι
είναι  . Κατόπιν επιλέχουμε
. Κατόπιν επιλέχουμε  τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε  έχουμε
έχουμε 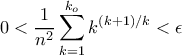 . Άρα τότε
. Άρα τότε 

 βρήκαμε ότι για
βρήκαμε ότι για  είναι
είναι  , Και λοιπά.
, Και λοιπά.![\displaystyle{ \displaystyle{ \dfrac {1}{n^{a+1}} \left ( [1^ad]+[2^ad]+[3^ad]+...+[n^ad]\right )} \displaystyle{ \displaystyle{ \dfrac {1}{n^{a+1}} \left ( [1^ad]+[2^ad]+[3^ad]+...+[n^ad]\right )}](/forum/ext/geomar/texintegr/latexrender/pictures/03935f6f0a46f72be3ea2c67401f3a47.png) , όπου
, όπου  και
και  πραγματικός.
πραγματικός.![[c] [c]](/forum/ext/geomar/texintegr/latexrender/pictures/26e45bc0a0d1de00c79246b858e0b7e8.png) δηλώνει ακέραιο μέρος.)
δηλώνει ακέραιο μέρος.) και
και  είναι ανοικτές).
είναι ανοικτές).Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 12 επισκέπτες