Σελίδα 1 από 1
Σειρά Pell - Lucas
Δημοσιεύτηκε: Σάβ Φεβ 22, 2020 12:18 am
από Tolaso J Kos
Οι
αριθμοί Pell - Lucas 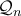
ορίζονται ως εξής:

και για κάθε

ισχύει η σχέση:

Να δειχθεί ότι:
 (H. Ohtsuka)
(H. Ohtsuka)
Re: Σειρά Pell - Lucas
Δημοσιεύτηκε: Δευ Νοέμ 01, 2021 7:43 am
από Tolaso J Kos
Επαναφορά.
Re: Σειρά Pell - Lucas
Δημοσιεύτηκε: Δευ Νοέμ 01, 2021 7:56 pm
από Mihalis_Lambrou
.
H πληκτρολόγιση είναι πάρα πολύ επίπονη, οπότε δίνω μόνο τα κύρια βήματα υπό μορφή εκτενούς υπόδειξης. Tην αντιγράφω από τις σημειώσεις μου, καθώς την είχα λύσει όταν προτάθηκε στο φόρουμ τον Φεβρουάριο αλλά δεν την ανάρτησα λόγω φόρτου εργασίας τότε.
α) Λύνοντας την αναδρομική σχέση θα βρούμε

(άμεσο και γνωστό)
β) Παίρνοντας δύο-δύο τους όρους σειρά γράφεται

γ) Από τον τύπο

είναι

και

δ) Από το γ) ο γενικός όρος του αθροίσματος είναι
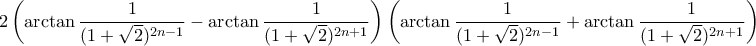
ε) Το άθροισμα είναι τηλεσκοπικό (πρέπει πρώτα να γράψουμε τον όρο ως διαφορά τετραγώνων). Μένει μόνο ο πρώτος όρος, δηλαδή

, το οποίο ισούται με το ζητούμενο.
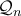 ορίζονται ως εξής:
ορίζονται ως εξής:  και για κάθε
και για κάθε  ισχύει η σχέση:
ισχύει η σχέση:

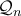 ορίζονται ως εξής:
ορίζονται ως εξής:  και για κάθε
και για κάθε  ισχύει η σχέση:
ισχύει η σχέση:

 (άμεσο και γνωστό)
(άμεσο και γνωστό)
 είναι
είναι  και
και 
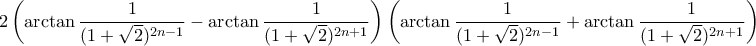
 , το οποίο ισούται με το ζητούμενο.
, το οποίο ισούται με το ζητούμενο.