
Ολοκλήρωμα
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ολοκλήρωμα
Ξεκινάμε με τη βασική σχέση:

οπότε το ολοκλήρωμά μας γράφεται ως:
![\displaystyle{\begin{aligned}
\int_{-1}^{1} \frac{\mathrm{d}x}{\sqrt{1+x} + \sqrt{1-x} + 2} &= \int_{-1}^{1} \frac{\mathrm{d}x}{\sqrt{2\left (1+\sqrt{1-x^2} \right )}+2} \\
&\!\!\!\!\!\overset{x = \sin u}{=\! =\! =\! =\! =\!} \int_{-\pi/2}^{\pi/2} \frac{\cos u}{\sqrt{2\left ( 1+\cos u \right )}+2}\, \mathrm{d}u\\
&=\int_{-\pi/2}^{\pi/2} \frac{\cos u}{\sqrt{4 \cos^2 \frac{u}{2}}+2} \, \mathrm{d}u \\
&= \int_{-\pi/2}^{\pi/2} \frac{\cos u}{2 \cos \frac{u}{2} + 2} \, \mathrm{d} u \\
&= \frac{1}{2} \int_{-\pi/2}^{\pi/2} \frac{\cos u}{1+ \cos \frac{u}{2}} \, \mathrm{d}u \\
&= \frac{1}{4} \int_{-\pi/2}^{\pi/2} \frac{\cos u}{\cos^2 \frac{u}{4}} \, \mathrm{d}u \\
&= \cancelto{0}{\frac{1}{4} \left [ 4 \tan \frac{u}{4} \cos u \right ]_{-\pi/2}^{\pi/2}} + \int_{-\pi/2}^{\pi/2} \tan \frac{u}{4} \sin u \, \mathrm{d}u
\end{aligned}} \displaystyle{\begin{aligned}
\int_{-1}^{1} \frac{\mathrm{d}x}{\sqrt{1+x} + \sqrt{1-x} + 2} &= \int_{-1}^{1} \frac{\mathrm{d}x}{\sqrt{2\left (1+\sqrt{1-x^2} \right )}+2} \\
&\!\!\!\!\!\overset{x = \sin u}{=\! =\! =\! =\! =\!} \int_{-\pi/2}^{\pi/2} \frac{\cos u}{\sqrt{2\left ( 1+\cos u \right )}+2}\, \mathrm{d}u\\
&=\int_{-\pi/2}^{\pi/2} \frac{\cos u}{\sqrt{4 \cos^2 \frac{u}{2}}+2} \, \mathrm{d}u \\
&= \int_{-\pi/2}^{\pi/2} \frac{\cos u}{2 \cos \frac{u}{2} + 2} \, \mathrm{d} u \\
&= \frac{1}{2} \int_{-\pi/2}^{\pi/2} \frac{\cos u}{1+ \cos \frac{u}{2}} \, \mathrm{d}u \\
&= \frac{1}{4} \int_{-\pi/2}^{\pi/2} \frac{\cos u}{\cos^2 \frac{u}{4}} \, \mathrm{d}u \\
&= \cancelto{0}{\frac{1}{4} \left [ 4 \tan \frac{u}{4} \cos u \right ]_{-\pi/2}^{\pi/2}} + \int_{-\pi/2}^{\pi/2} \tan \frac{u}{4} \sin u \, \mathrm{d}u
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/1cffac8d6ee91ed06963cd6ec67eb052.png)
Φτάνουμε λοιπόν έτσι σε κάτι πιο απλό το οποίο είναι αρκετά αντιμετωπίσιμο !
Για παράδειγμα:

διότι

και

Η φαντασία είναι σημαντικότερη από τη γνώση !


Re: Ολοκλήρωμα
Γεια χαρά σε όλους. Άλλη μια ιδέα είναι η ακόλουθη. Επειδή η ολοκληρωτέα συνάρτηση είναι άρτια στο ![\displaystyle{\left[-1,1\right]} \displaystyle{\left[-1,1\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/7a82e4bfff7de433dc3bfbf57bf7d83a.png) αρκεί να υπολογίσουμε το ολοκλήρωμα
αρκεί να υπολογίσουμε το ολοκλήρωμα 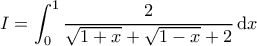
Με αντικατάσταση![\displaystyle{x=\cos\,(2\,t)\,t\in\left[0,\dfrac{\pi}{4}\right] \displaystyle{x=\cos\,(2\,t)\,t\in\left[0,\dfrac{\pi}{4}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/8f40cd05892834f4e12ce9c230b26963.png) βρίσκουμε
βρίσκουμε  και επιπλέον,
και επιπλέον,
 οπότε έχουμε
οπότε έχουμε
![\displaystyle{\begin{aligned} I&=\int_{\pi/4}^{0}\dfrac{4\,\sin\,(2\,t)}{\,\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\,\mathrm{d}t\\&=2\,\int_{0}^{\pi/4}\dfrac{2\,\sin\,(2\,t)}{\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\,\mathrm{d}t\\&=2\,\int_{0}^{\pi/4}\dfrac{(\sqrt{2}\,cos\,t+\sqrt{2}\,\sin\,t+2)^2-4\,(\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2)+2}{\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\\&=2\,\int_{0}^{\pi/4}\left(\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2)\right)\,\mathrm{d}t-8\,\int_{0}^{\pi/4}\,\mathrm{d}t+\int_{0}^{\pi/4}\dfrac{4}{2\,\cos\,\left(t-\dfrac{\pi}{4}\right)+2}\,\mathrm{d}t\\&=2\,\left[\sqrt{2}\,\sin\,t-\sqrt{2}\,\cos\,t+2\,t\right]_{0}^{\pi/4}-8\,\dfrac{\pi}{4}+2\,\int_{0}^{\pi/4}\dfrac{1}{2\,\cos^2\,\left(\dfrac{t}{2}-\dfrac{\pi}{8}\right)}\,\mathrm{d}t\\&=\pi-2\,\pi+2\,\sqrt{2}+2\,\left[\tan\,\left(\dfrac{t}{2}-\dfrac{\pi}{8}\right)\right]_{0}^{\pi/4}\\&=2\,\sqrt{2}-\pi+2\,\tan\,\left(\dfrac{\pi}{8}\right)\,\,(1)\end{aligned} \displaystyle{\begin{aligned} I&=\int_{\pi/4}^{0}\dfrac{4\,\sin\,(2\,t)}{\,\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\,\mathrm{d}t\\&=2\,\int_{0}^{\pi/4}\dfrac{2\,\sin\,(2\,t)}{\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\,\mathrm{d}t\\&=2\,\int_{0}^{\pi/4}\dfrac{(\sqrt{2}\,cos\,t+\sqrt{2}\,\sin\,t+2)^2-4\,(\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2)+2}{\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\\&=2\,\int_{0}^{\pi/4}\left(\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2)\right)\,\mathrm{d}t-8\,\int_{0}^{\pi/4}\,\mathrm{d}t+\int_{0}^{\pi/4}\dfrac{4}{2\,\cos\,\left(t-\dfrac{\pi}{4}\right)+2}\,\mathrm{d}t\\&=2\,\left[\sqrt{2}\,\sin\,t-\sqrt{2}\,\cos\,t+2\,t\right]_{0}^{\pi/4}-8\,\dfrac{\pi}{4}+2\,\int_{0}^{\pi/4}\dfrac{1}{2\,\cos^2\,\left(\dfrac{t}{2}-\dfrac{\pi}{8}\right)}\,\mathrm{d}t\\&=\pi-2\,\pi+2\,\sqrt{2}+2\,\left[\tan\,\left(\dfrac{t}{2}-\dfrac{\pi}{8}\right)\right]_{0}^{\pi/4}\\&=2\,\sqrt{2}-\pi+2\,\tan\,\left(\dfrac{\pi}{8}\right)\,\,(1)\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/7f83bfa62c8007444a4621178641c971.png)
όπου από τη γνωστή σχέση έχουμε για
έχουμε για  ότι
ότι
 και με διακρίνουσα βρίσκουμε ότι
και με διακρίνουσα βρίσκουμε ότι 
Τελικά, από σχέση παίρνουμε
παίρνουμε 
![\displaystyle{\left[-1,1\right]} \displaystyle{\left[-1,1\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/7a82e4bfff7de433dc3bfbf57bf7d83a.png) αρκεί να υπολογίσουμε το ολοκλήρωμα
αρκεί να υπολογίσουμε το ολοκλήρωμα 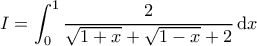
Με αντικατάσταση
![\displaystyle{x=\cos\,(2\,t)\,t\in\left[0,\dfrac{\pi}{4}\right] \displaystyle{x=\cos\,(2\,t)\,t\in\left[0,\dfrac{\pi}{4}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/8f40cd05892834f4e12ce9c230b26963.png) βρίσκουμε
βρίσκουμε  και επιπλέον,
και επιπλέον,  οπότε έχουμε
οπότε έχουμε![\displaystyle{\begin{aligned} I&=\int_{\pi/4}^{0}\dfrac{4\,\sin\,(2\,t)}{\,\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\,\mathrm{d}t\\&=2\,\int_{0}^{\pi/4}\dfrac{2\,\sin\,(2\,t)}{\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\,\mathrm{d}t\\&=2\,\int_{0}^{\pi/4}\dfrac{(\sqrt{2}\,cos\,t+\sqrt{2}\,\sin\,t+2)^2-4\,(\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2)+2}{\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\\&=2\,\int_{0}^{\pi/4}\left(\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2)\right)\,\mathrm{d}t-8\,\int_{0}^{\pi/4}\,\mathrm{d}t+\int_{0}^{\pi/4}\dfrac{4}{2\,\cos\,\left(t-\dfrac{\pi}{4}\right)+2}\,\mathrm{d}t\\&=2\,\left[\sqrt{2}\,\sin\,t-\sqrt{2}\,\cos\,t+2\,t\right]_{0}^{\pi/4}-8\,\dfrac{\pi}{4}+2\,\int_{0}^{\pi/4}\dfrac{1}{2\,\cos^2\,\left(\dfrac{t}{2}-\dfrac{\pi}{8}\right)}\,\mathrm{d}t\\&=\pi-2\,\pi+2\,\sqrt{2}+2\,\left[\tan\,\left(\dfrac{t}{2}-\dfrac{\pi}{8}\right)\right]_{0}^{\pi/4}\\&=2\,\sqrt{2}-\pi+2\,\tan\,\left(\dfrac{\pi}{8}\right)\,\,(1)\end{aligned} \displaystyle{\begin{aligned} I&=\int_{\pi/4}^{0}\dfrac{4\,\sin\,(2\,t)}{\,\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\,\mathrm{d}t\\&=2\,\int_{0}^{\pi/4}\dfrac{2\,\sin\,(2\,t)}{\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\,\mathrm{d}t\\&=2\,\int_{0}^{\pi/4}\dfrac{(\sqrt{2}\,cos\,t+\sqrt{2}\,\sin\,t+2)^2-4\,(\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2)+2}{\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2}\\&=2\,\int_{0}^{\pi/4}\left(\sqrt{2}\,\cos\,t+\sqrt{2}\,\sin\,t+2)\right)\,\mathrm{d}t-8\,\int_{0}^{\pi/4}\,\mathrm{d}t+\int_{0}^{\pi/4}\dfrac{4}{2\,\cos\,\left(t-\dfrac{\pi}{4}\right)+2}\,\mathrm{d}t\\&=2\,\left[\sqrt{2}\,\sin\,t-\sqrt{2}\,\cos\,t+2\,t\right]_{0}^{\pi/4}-8\,\dfrac{\pi}{4}+2\,\int_{0}^{\pi/4}\dfrac{1}{2\,\cos^2\,\left(\dfrac{t}{2}-\dfrac{\pi}{8}\right)}\,\mathrm{d}t\\&=\pi-2\,\pi+2\,\sqrt{2}+2\,\left[\tan\,\left(\dfrac{t}{2}-\dfrac{\pi}{8}\right)\right]_{0}^{\pi/4}\\&=2\,\sqrt{2}-\pi+2\,\tan\,\left(\dfrac{\pi}{8}\right)\,\,(1)\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/7f83bfa62c8007444a4621178641c971.png)
όπου από τη γνωστή σχέση
 έχουμε για
έχουμε για  ότι
ότι  και με διακρίνουσα βρίσκουμε ότι
και με διακρίνουσα βρίσκουμε ότι 
Τελικά, από σχέση
 παίρνουμε
παίρνουμε 
Παπαπέτρος Ευάγγελος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
