Δίνεται η ακολουθία πραγματικών
 για την οποία ισχύουν
για την οποία ισχύουν 
και
 για κάθε
για κάθε 
Να δείξετε ότι
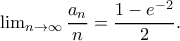
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 για την οποία ισχύουν
για την οποία ισχύουν 
 για κάθε
για κάθε 
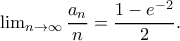
Λάμπρος Κατσάπας έγραψε: ↑Σάβ Ιούλ 11, 2020 7:01 pmΠροέκυψε από πρόβλημα...
Δίνεται η ακολουθία πραγματικώνγια την οποία ισχύουν

καιγια κάθε

Να δείξετε ότι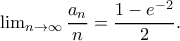
Και εγώ την ακολουθία βρήκα με standard διαδικασία.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Ιούλ 17, 2020 9:52 amΛάμπρος Κατσάπας έγραψε: ↑Σάβ Ιούλ 11, 2020 7:01 pmΠροέκυψε από πρόβλημα...
Δίνεται η ακολουθία πραγματικώνγια την οποία ισχύουν

καιγια κάθε

Να δείξετε ότι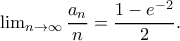





 και παραγωγίζοντας οδηγούμαστε
και παραγωγίζοντας οδηγούμαστε  η οποία, κατά τα γνωστά, δίνει τελικά
η οποία, κατά τα γνωστά, δίνει τελικά Ο υπολογισμός της σταθεράς που προκύπτει κατά την επίλυση της
Ο υπολογισμός της σταθεράς που προκύπτει κατά την επίλυση της 



 και παίρνοντας όριο έχουμε το ζητούμενο.
και παίρνοντας όριο έχουμε το ζητούμενο. συγκλίνει)
συγκλίνει)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες