 .
. - Χρησιμοποιώντας το extended binomial theorem αναπτύξτε τη συνάρτηση
 σε σειρά Fourier συνημιτόνων.
σε σειρά Fourier συνημιτόνων. - Να δειχθεί η ταυτότητα:

όπου η συνάρτηση Γάμμα του Euler.
η συνάρτηση Γάμμα του Euler.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 .
.  σε σειρά Fourier συνημιτόνων.
σε σειρά Fourier συνημιτόνων.
 η συνάρτηση Γάμμα του Euler.
η συνάρτηση Γάμμα του Euler.
Τόλη γράψε σωστά την εκφώνηση.Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 9:58 pmΈστω.
- Χρησιμοποιώντας το extended binomial theorem αναπτύξτε τη συνάρτηση
σε σειρά Fourier συνημιτόνων.
- Να δειχθεί η ταυτότητα:

όπουη συνάρτηση Γάμμα του Euler.
 ;
; ισχύει η ταυτότητα.
ισχύει η ταυτότητα. . Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα
. Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα  .
.
Δεν το είδα.Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 11:10 pmΜα Σταύρο στο ορίζω το. Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα
.

 .
.
 και στο
και στο 
Σίγουρα;Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 9:58 pmΈστω.
- Χρησιμοποιώντας το extended binomial theorem αναπτύξτε τη συνάρτηση
σε σειρά Fourier συνημιτόνων.
- Να δειχθεί η ταυτότητα:

όπουη συνάρτηση Γάμμα του Euler.
 πρέπει να γίνει
πρέπει να γίνει  (αλλά τότε δεν είναι σειρά Fourier).
(αλλά τότε δεν είναι σειρά Fourier).  τον τυπικό συντελεστή τότε
τον τυπικό συντελεστή τότε 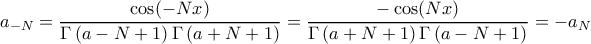
 .
.
 είναι σε δυνάμεις).
είναι σε δυνάμεις).  και
και  . Είναι:
. Είναι:

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιούλ 14, 2020 11:49 pmΔεν το είδα.Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 11:10 pmΜα Σταύρο στο ορίζω το. Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα
.
Και ο λόγος είναι γιατί τότε πρέπει να περιορίσεις τα
Η ταυτότητα αποκλείεται να ισχύει στο.
Πρόσεξε το
δεν οριζεται στοκαι στο
δεν είναι μονοσήμαντα ορισμένο.
 που ορίζεται.
που ορίζεται.Extended Binomial Theorem έγραψε:

Καλημέρα από την Χαλκίδα.Tolaso J Kos έγραψε: ↑Τετ Ιούλ 15, 2020 10:17 amΗ ταυτότητα έχει ελεγχθεί με το W|A για διάφορες τιμές τωνκαι
. Είναι:

Οπότε,
 ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιούλ 14, 2020 11:49 pmΔεν το είδα.Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 11:10 pmΜα Σταύρο στο ορίζω το
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιούλ 14, 2020 11:49 pmΔεν το είδα.Tolaso J Kos έγραψε: ↑Τρί Ιούλ 14, 2020 11:10 pmΜα Σταύρο στο ορίζω το. Είναι πραγματικός. Η ταυτότητα ισχύει για όλα τα
.
Και ο λόγος είναι γιατί τότε πρέπει να περιορίσεις τα
Η ταυτότητα αποκλείεται να ισχύει στο.
Πρόσεξε το
δεν οριζεται στοκαι στο
δεν είναι μονοσήμαντα ορισμένο.
Ας βάλουμε για ταπου ορίζεται.
Extended Binomial Theorem έγραψε:
Από ότι είδα στην παραπομπή ο τύπος ισχύει για μιγαδικάExtended Binomial Theorem έγραψε:

 έχει πόλους.
έχει πόλους. ;
; ;
;Νομίζω ότι θα χάσουμε την μπάλα.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες