 γραμμικὸς ὑπόχωρος τοῦ
γραμμικὸς ὑπόχωρος τοῦ ![C[a,b] C[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/d930e3053f32dbc51f14e870df59674d.png) πεπερασμένης διαστάσεως καὶ
πεπερασμένης διαστάσεως καὶ ![\{f_n\}\subset C[a,b] \{f_n\}\subset C[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/cf5c78a9f63a7e6bda08daf281b12570.png) . Ἄν ἡ ἀκολουθία
. Ἄν ἡ ἀκολουθία  συγκλίνει κατὰ σημεῖον, τότε συγκλίνει καὶ ὁμοιόμορφα.
συγκλίνει κατὰ σημεῖον, τότε συγκλίνει καὶ ὁμοιόμορφα.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 γραμμικὸς ὑπόχωρος τοῦ
γραμμικὸς ὑπόχωρος τοῦ ![C[a,b] C[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/d930e3053f32dbc51f14e870df59674d.png) πεπερασμένης διαστάσεως καὶ
πεπερασμένης διαστάσεως καὶ ![\{f_n\}\subset C[a,b] \{f_n\}\subset C[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/cf5c78a9f63a7e6bda08daf281b12570.png) . Ἄν ἡ ἀκολουθία
. Ἄν ἡ ἀκολουθία  συγκλίνει κατὰ σημεῖον, τότε συγκλίνει καὶ ὁμοιόμορφα.
συγκλίνει κατὰ σημεῖον, τότε συγκλίνει καὶ ὁμοιόμορφα.Νομίζω ότι υπάρχει τυπογραφικό στην εκφώνηση.Γ.-Σ. Σμυρλής έγραψε: ↑Σάβ Δεκ 04, 2021 7:02 pmΠΡΟΒΛΗΜΑ. Ἔστωγραμμικὸς ὑπόχωρος τοῦ
πεπερασμένης διαστάσεως καὶ
. Ἄν ἡ ἀκολουθία
συγκλίνει κατὰ σημεῖον, τότε συγκλίνει καὶ ὁμοιόμορφα.
 γραμμικὸς ὑπόχωρος τοῦ
γραμμικὸς ὑπόχωρος τοῦ ![C[a,b] C[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/d930e3053f32dbc51f14e870df59674d.png) πεπερασμένης διαστάσεως καὶ
πεπερασμένης διαστάσεως καὶ  . Ἄν ἡ ἀκολουθία
. Ἄν ἡ ἀκολουθία  συγκλίνει κατὰ σημεῖον, τότε συγκλίνει καὶ ὁμοιόμορφα.
συγκλίνει κατὰ σημεῖον, τότε συγκλίνει καὶ ὁμοιόμορφα.


 στο
στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) ώστε
ώστε 

 για σταθερό
για σταθερό 



![sup \left \{ |g_i(x)|:x\in [a,b] \right \} sup \left \{ |g_i(x)|:x\in [a,b] \right \}](/forum/ext/geomar/texintegr/latexrender/pictures/506d1717416407ce21792cf3c950f2d2.png)
 παίρνουμε
παίρνουμε 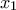 ώστε
ώστε 

![x\in [a,b] x\in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/8290bddba5acf9822dcbf61f4ac67d1b.png) εχουμε άτοπο λόγω γραμμικής ανεξαρτησίας.
εχουμε άτοπο λόγω γραμμικής ανεξαρτησίας. με
με 
 .
.
 για
για 
 για
για  και
και 
 για όλα τα
για όλα τα ![x\in [a,b] x\in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/8290bddba5acf9822dcbf61f4ac67d1b.png) εχουμε άτοπο λόγω γραμμικής ανεξαρτησίας.
εχουμε άτοπο λόγω γραμμικής ανεξαρτησίας.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 15 επισκέπτες