Ένα άθροισμα

Tolaso J Kos · #1

Να υπολογιστεί το άθροισμα $\displaystyle{\sum_{\substack{n =1 \\ n \neq m}}^{\infty} \frac{1}{m^2-n^2}}$ .

#2

Tolaso J Kos έγραψε: ↑
Κυρ Μάιος 22, 2022 12:24 pm
Να υπολογιστεί το άθροισμα $\displaystyle{\sum_{\substack{n =1 \\ n \neq m}}^{\infty} \frac{1}{m^2-n^2}}$ .

Απάντηση: $-\dfrac {3}{4m^2}$

Χωρίζουμε το άθροισμα σε δύο μέρη, τα n<m

και

. Δηλαδή το γράφουμε ως $\displaystyle{ \sum_{\substack{n =1 }}^{m-1} \frac{1}{m^2-n^2} + \sum _{\substack{n =m+1 }}^{\infty} \frac{1}{m^2-n^2}}}$ .

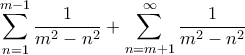α) Το πρώτο γράφεται $\displaystyle{ \dfrac {1}{2m} \sum_{\substack{n =1 }}^{m-1} \left ( \dfrac{1}{m-n} + \dfrac {1}{m+n} \right )}$ . Γράφοντας το πρώτο ανάποδα, η όλη παράσταση ισούται

$\displaystyle{ \dfrac {1}{2m} \sum_{\substack{n =1 }}^{m-1} \dfrac{1}{n} + \dfrac {1}{2m} \sum_{\substack{n =m+1 }}^{2m-1} \dfrac {1}{n} = \dfrac {1}{2m} \sum_{\substack{n =1 \\ n \neq m }}^{2m-1} \dfrac{1}{n}}$

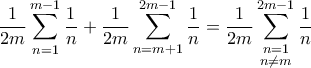
β) Το δεύτερο γράφεται (θα το γράφω ως κάποιο μεγάλο

και στο τέλος θα πάροuμε όριο $N\to \infty$ )

$\displaystyle{ \dfrac {1}{2m} \sum_{\substack{n =m+1 }}^{N} \left ( \dfrac{1}{m-n} + \dfrac {1}{m+n} \right )= \dfrac {1}{2m} \sum_{\substack{n =m+1 }}^{N} \dfrac{1}{m-n} + \dfrac {1}{2m} \sum_{\substack{n =m+1 }}^{N} \dfrac {1}{m+n}= - \dfrac {1}{2m} \sum_{\substack{n =1 }}^{N-m} \dfrac {1}{n} + \dfrac {1}{2m} \sum_{\substack{n =2m+1 }}^{N+m} \dfrac{1}{n}}$

Απλοποιούμε τώρα τους όρους που εμφανίζονται μια φορά με "πλην" και μια με "συν". Μένει

$\displaystyle{- \dfrac {1}{2m} \sum_{\substack{n =1 }}^{2m} \dfrac {1}{n} + \dfrac {1}{2m} \sum_{\substack{n =N-m+1 }}^{N+m} \dfrac{1}{n}}$

Όταν πάρουμε όριο $N\to \infty$ το τελευταίο άθροισμα, που αποτελείται από

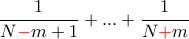όρους $\dfrac {1}{N{\color {red} -}m+1}+...+\dfrac {1}{N{\color {red} +}m}$ τείνει στο

.

Συνοψίζοντας, μετά το όριο, το αρχικό μας άθροισμα είναι το τμήμα που βρήκαμε στο α) μέρος και το κομμάτι που περίσσεψε στο β). Δηλαδή είναι

$\displaystyle{\dfrac {1}{2m} \sum_{\substack{n =1 \\ n \neq m }}^{2m-1} \dfrac{1}{n}- \dfrac {1}{2m} \sum_{\substack{n =1 }}^{2m} \dfrac {1}{n}}$

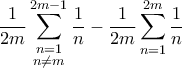
από όπου απλοποιούνται όλοι οι όροι εκτός από δύο, τους n=m

και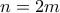

. Μένει λοιπόν

$\displaystyle{\dfrac {1}{2m} \left (- \dfrac {1}{m} - \dfrac {1}{2m} \right ) = -\dfrac {3}{4m^2} }$

Σχόλιο: Θα μπορούσα να εργαστώ με συναρτήσεις $\psi$ για τυπογραφική ευκολία, αλλά επειδή δεν αλλάζει η ουσία προτίμησα τρόπο που θα ήταν κατανοητός σε φοιτητή στα πρώτα εξάμηνα σπουδών.

Tolaso J Kos · #3

Mihalis_Lambrou έγραψε: ↑
Δευ Μάιος 23, 2022 10:38 pm
Σχόλιο: Θα μπορούσα να εργαστώ με συναρτήσεις $\psi$ για τυπογραφική ευκολία, αλλά επειδή δεν αλλάζει η ουσία προτίμησα τρόπο που θα ήταν κατανοητός σε φοιτητή στα πρώτα εξάμηνα σπουδών.

Άποψή μου πάντα ότι και αυτή τη λύση φοιτητές των πρώτων εξάμηνων σπουδών ... δε θα τη καταλάβαιναν... !!

#4

Tolaso J Kos έγραψε: ↑
Τρί Μάιος 24, 2022 12:38 pm
Άποψή μου πάντα ότι και αυτή τη λύση φοιτητές των πρώτων εξάμηνων σπουδών ... δε θα τη καταλάβαιναν... !!

Δεν μιλάμε για φοιτητές που δεν ξέρουν το (a+b)^2 =a^2+2ab+b^2

(δυστυχώς μη αμελητέο ποσοστό) αλλά εκείνους που έχουν κάποια βασική Μαθηματική στόφα (ευτυχώς υπάρχουν αρκετοί). Οι φοιτητές που τα Μαθηματικά τους είναι στο επίπεδο της παπαγαλίας, πράγματι δεν θα καταλάβουν την απόδειξη, παρ' όλο που στην πραγματικότητα είναι απλή.

Αν θέλει κανείς να την καταλάβει μπορεί να πάρει το

κάποιον μικρό αριθμό, π.χ. m=5

, και να ακολουθήσει τα βήματα. Είναι όλα προφανή, ιδίως αν γράψει κανείς τους προσθετέους σε στήλες. Η μόνη τεχνική δυσκολία είναι το γεγονός ότι εμφανίζεται η αποκλίνουσα $\displaystyle{\sum_{n=1}^{\infty } \dfrac {1}{n}}$ , οπότε δεν μπορούμε να κάνουμε στα τυφλά την αναδιάταξη των προσθετέων. Παρακάμπτουμε την δυσκολία με το να δουλέψουμε με πεπερασμένα αθροίσματα $\displaystyle{\sum_{n=1}^N \dfrac {1}{n}}$ και στο τέλος να πάρουμε όρια (που υπάρχουν γιατί οι πολλοί όροι έχουν απλοποιηθεί).

#5

Mihalis_Lambrou έγραψε: ↑
Τρί Μάιος 24, 2022 1:50 pm
Αν θέλει κανείς να την καταλάβει μπορεί να πάρει το κάποιον μικρό αριθμό, π.χ. , και να ακολουθήσει τα βήματα. Είναι όλα προφανή, ιδίως αν γράψει κανείς τους προσθετέους σε στήλες.

Για να γίνει απόλυτα σαφές τι εννοώ, το θέτω ως άσκηση:

Δείξτε ότι $\displaystyle{\sum_{n=6}^{\infty} \dfrac {1}{n^2-5^2} = \dfrac {1}{10}+ \dfrac {1}{20}+ \dfrac {1}{30}+...+\dfrac {1}{100}}$ .
H απόδειξη πρέπει να είναι κατανοητή και προσιτή στον φοιτητή του πρώτου εξαμήνου, που μόλις έμαθε λίγα πράγματα για σειρές.

stranger · #6

Mihalis_Lambrou έγραψε: ↑
Τρί Μάιος 24, 2022 1:50 pm
Η μόνη τεχνική δυσκολία είναι το γεγονός ότι εμφανίζεται η αποκλίνουσα $\displaystyle{\sum_{n=1}^{\infty } \dfrac {1}{n}}$ , οπότε δεν μπορούμε να κάνουμε στα τυφλά την αναδιάταξη των προσθετέων. Παρακάμπτουμε την δυσκολία με το να δουλέψουμε με πεπερασμένα αθροίσματα $\displaystyle{\sum_{n=1}^N \dfrac {1}{n}}$

Κύριε Λάμπρου ένα σχόλιο πάνω σε αυτό.
Σε οποιαδήποτε σειρά με θετικούς όρους παραμένει ίδια η τιμή της οποιαδήποτε αναδιάταξη και να της κάνουμε, ακόμα και αν αυτή αποκλίνει.

#7

stranger έγραψε: ↑
Τετ Μάιος 25, 2022 11:31 am
Σε οποιαδήποτε σειρά με θετικούς όρους παραμένει ίδια η τιμή της οποιαδήποτε αναδιάταξη και να της κάνουμε, ακόμα και αν αυτή αποκλίνει.

Σωστά, αλλά εδώ δεν έχουμε μόνο θετικούς όρους. Αυτή που αναδιατάσουμε δεν είναι η $\displaystyle{\sum_{n=6}^{\infty} \dfrac {1}{n^2-5^2}}$ στην μορφή της

$\displaystyle{\dfrac {1}{10} \sum_{n=6}^{\infty}\left ( \dfrac {1}{n-5} - \dfrac {1}{n+5} \right ) }$ αλλά των

$\displaystyle{\dfrac {1}{10} \sum_{n=6}^{\infty} \dfrac {1}{n-5}- \dfrac {1}{10} \sum_{n=6}^{\infty} \dfrac {1}{n+5}}$

ανακατεύοντάς τους προσθετέους μεταξύ των. Γι' αυτό προτίμησα άθροισμα από

έως

, όπου δεν προκύπτουν προβλήματα.

stranger · #8

Mihalis_Lambrou έγραψε: ↑
Τετ Μάιος 25, 2022 12:43 pm

stranger έγραψε: ↑
Τετ Μάιος 25, 2022 11:31 am
Σε οποιαδήποτε σειρά με θετικούς όρους παραμένει ίδια η τιμή της οποιαδήποτε αναδιάταξη και να της κάνουμε, ακόμα και αν αυτή αποκλίνει.
Σωστά, αλλά εδώ δεν έχουμε μόνο θετικούς όρους. Αυτή που αναδιατάσουμε δεν είναι η $\displaystyle{\sum_{n=6}^{\infty} \dfrac {1}{n^2-5^2}}$ στην μορφή της

$\displaystyle{\dfrac {1}{10} \sum_{n=6}^{\infty}\left ( \dfrac {1}{n-5} - \dfrac {1}{n+5} \right ) }$ αλλά των

$\displaystyle{\dfrac {1}{10} \sum_{n=6}^{\infty} \dfrac {1}{n-5}- \dfrac {1}{10} \sum_{n=6}^{\infty} \dfrac {1}{n+5}}$

ανακατεύοντάς τους προσθετέους μεταξύ των. Γι' αυτό προτίμησα άθροισμα από έως , όπου δεν προκύπτουν προβλήματα.

Εντάξει.Τώρα είναι σαφές.Ευχαριστώ.

Ένα άθροισμα

Ένα άθροισμα

Re: Ένα άθροισμα

Re: Ένα άθροισμα

Re: Ένα άθροισμα

Re: Ένα άθροισμα

Re: Ένα άθροισμα

Re: Ένα άθροισμα

Re: Ένα άθροισμα

Μέλη σε σύνδεση