- Έστω
 πραγματικός αριθμός. Να δειχθεί ότι
πραγματικός αριθμός. Να δειχθεί ότι 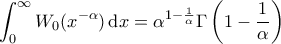 .
. - Να δειχθεί ότι
 .
.
Μπορούν να χρησιμοποιηθούν οι τύποι MacLaurent για τη συνάρτηση Lambert.
Άσκηση 2 (Μετασχηματισμός Mellin)
Να δειχθεί ότι για κάθε πραγματικό αριθμό
 ισχύει
ισχύει  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 πραγματικός αριθμός. Να δειχθεί ότι
πραγματικός αριθμός. Να δειχθεί ότι 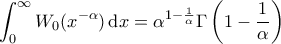 .
. .
.  ισχύει
ισχύει  .
.
Tolaso J Kos έγραψε: ↑Κυρ Ιούλ 17, 2022 3:04 pmΆσκηση 1
- Έστω
πραγματικός αριθμός. Να δειχθεί ότι
.
- Να δειχθεί ότι
.
Μπορούν να χρησιμοποιηθούν οι τύποι MacLaurent για τη συνάρτηση Lambert.
Άσκηση 2 (Μετασχηματισμός Mellin)
Να δειχθεί ότι για κάθε πραγματικό αριθμόισχύει
.
Όπως τα λέει ο Σταύρος. Έχουμε:ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Οκτ 16, 2022 2:42 pmTolaso J Kos έγραψε: ↑Κυρ Ιούλ 17, 2022 3:04 pmΆσκηση 1
- Έστω
πραγματικός αριθμός. Να δειχθεί ότι
.
- Να δειχθεί ότι
.
Μπορούν να χρησιμοποιηθούν οι τύποι MacLaurent για τη συνάρτηση Lambert.
![\displaystyle{\begin{aligned}
\int_{0}^{\infty} W_0\left ( x^{-\alpha} \right )\, \mathrm{d}x & \overset{t =W_0 \left ( x^{-\alpha} \right )}{=\! =\! =\! =\! =\! =\! =\! =\!} \frac{1}{\alpha} \int_{0}^{\infty} \left ( t+1 \right ) t^{-1/\alpha} e^{-t/\alpha}\, \mathrm{d}t \\
&\!\!\!\!\!\!\!\overset{t = \alpha s}{=\! =\! =\! =\! =\!} \alpha^{-1/\alpha} \int_{0}^{\infty} \left ( 1+ \alpha s \right ) s^{-1/\alpha} e^{-s}\, \mathrm{d}s \\
&= \alpha^{-1/\alpha} \left ( \int_{0}^{\infty} \alpha^{-1/\alpha} e^{-s}\, \mathrm{d}s + \alpha \int_{0}^{\infty} s^{1-1/\alpha} e^{-s} \, \mathrm{d}s \right ) \\
&= \alpha^{-1/\alpha} \left [ \Gamma \left ( 1 - \frac{1}{\alpha} \right ) + \alpha \Gamma \left ( 2 - \frac{1}{\alpha} \right ) \right ] \\
&= \alpha^{-1/\alpha} \left [ \Gamma \left ( 1 - \frac{1}{\alpha} \right ) + \alpha \left ( 1 - \frac{1}{\alpha} \right ) \Gamma \left ( 1 - \frac{1}{\alpha} \right ) \right ] \\
&= \alpha^{1 - 1/\alpha} \Gamma \left ( 1 - \frac{1}{\alpha} \right )
\end{aligned}} \displaystyle{\begin{aligned}
\int_{0}^{\infty} W_0\left ( x^{-\alpha} \right )\, \mathrm{d}x & \overset{t =W_0 \left ( x^{-\alpha} \right )}{=\! =\! =\! =\! =\! =\! =\! =\!} \frac{1}{\alpha} \int_{0}^{\infty} \left ( t+1 \right ) t^{-1/\alpha} e^{-t/\alpha}\, \mathrm{d}t \\
&\!\!\!\!\!\!\!\overset{t = \alpha s}{=\! =\! =\! =\! =\!} \alpha^{-1/\alpha} \int_{0}^{\infty} \left ( 1+ \alpha s \right ) s^{-1/\alpha} e^{-s}\, \mathrm{d}s \\
&= \alpha^{-1/\alpha} \left ( \int_{0}^{\infty} \alpha^{-1/\alpha} e^{-s}\, \mathrm{d}s + \alpha \int_{0}^{\infty} s^{1-1/\alpha} e^{-s} \, \mathrm{d}s \right ) \\
&= \alpha^{-1/\alpha} \left [ \Gamma \left ( 1 - \frac{1}{\alpha} \right ) + \alpha \Gamma \left ( 2 - \frac{1}{\alpha} \right ) \right ] \\
&= \alpha^{-1/\alpha} \left [ \Gamma \left ( 1 - \frac{1}{\alpha} \right ) + \alpha \left ( 1 - \frac{1}{\alpha} \right ) \Gamma \left ( 1 - \frac{1}{\alpha} \right ) \right ] \\
&= \alpha^{1 - 1/\alpha} \Gamma \left ( 1 - \frac{1}{\alpha} \right )
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/9a4c7e7eec5f0b2eb8e34763f8acb71c.png)
![\displaystyle{W_0(x) = \sum_{n=1}^{\infty} \frac{(-n)^{n-1} x^n}{n!} \; , \; x \in \left [ -\frac{1}{e} , \frac{1}{e} \right ]} \displaystyle{W_0(x) = \sum_{n=1}^{\infty} \frac{(-n)^{n-1} x^n}{n!} \; , \; x \in \left [ -\frac{1}{e} , \frac{1}{e} \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/93cf469287301e92c231fcdc2cb5aa72.png) . Συνεπώς,
. Συνεπώς,


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες