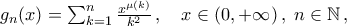είναι η συνάρτηση Möbius.
είναι η συνάρτηση Möbius.Σύγκλιση ακολουθιών συναρτήσεων
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Σύγκλιση ακολουθιών συναρτήσεων
Να εξετασθούν ως προς την σημειακή σύγκλιση οι ακολουθίες συναρτήσεων
 είναι η συνάρτηση Möbius.
είναι η συνάρτηση Möbius.
 είναι η συνάρτηση Möbius.
είναι η συνάρτηση Möbius.
Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Σύγκλιση ακολουθιών συναρτήσεων
α) Η πρώτη αποκλίνει για κάθε
 . Πράγματι, αφού όλοι οι όροι είναι θετικοί, έχουμε
. Πράγματι, αφού όλοι οι όροι είναι θετικοί, έχουμε  , διότι η σειρά πρώτων
, διότι η σειρά πρώτων  αποκλίνει.
αποκλίνει.β) Η δεύτερη συγκλίνει για κάθε
 . Πράγματι, αφού η
. Πράγματι, αφού η  παίρνει μόνο τις τιμές
παίρνει μόνο τις τιμές  έχουμε
έχουμε  . Άρα
. Άρα  , δηλαδή φραγμένο δεξί μέλος. Τελειώσαμε.
, δηλαδή φραγμένο δεξί μέλος. Τελειώσαμε.- Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σύγκλιση ακολουθιών συναρτήσεων
Μιχάλη,
νομίζω ότι η άσκηση δε ζητάει τη σύγκλιση/απόκλιση των ακολουθιών αλλά τη σημειακή σύγκλιση αυτών.
νομίζω ότι η άσκηση δε ζητάει τη σύγκλιση/απόκλιση των ακολουθιών αλλά τη σημειακή σύγκλιση αυτών.
Η φαντασία είναι σημαντικότερη από τη γνώση !


-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Σύγκλιση ακολουθιών συναρτήσεων
Τόλη, αυτό έκανα. 'Εδειξα για ποιαTolaso J Kos έγραψε: ↑Κυρ Νοέμ 27, 2022 1:07 amΜιχάλη,
νομίζω ότι η άσκηση δε ζητάει τη σύγκλιση/απόκλιση των ακολουθιών αλλά τη σημειακή σύγκλιση αυτών.
 συγκλίνουν ή απακλκίνουν. Άυτό ακριβώς είναι η σημειακή σύγκλιση ή μη.
συγκλίνουν ή απακλκίνουν. Άυτό ακριβώς είναι η σημειακή σύγκλιση ή μη.- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σύγκλιση ακολουθιών συναρτήσεων
Από όσα γνωρίζω, αλλά και από ότι διαισθάνομαι, δεν υπάρχει τύπος (σε κλειστή μορφή) για το άθροισμα  , έστω και για κάποιο συγκεκριμένο
, έστω και για κάποιο συγκεκριμένο  . Αν γνωρίζει κάποιος κάτι επ' αυτού, θα ήταν ενδιαφέρον να το μάθουμε.
. Αν γνωρίζει κάποιος κάτι επ' αυτού, θα ήταν ενδιαφέρον να το μάθουμε.
 , έστω και για κάποιο συγκεκριμένο
, έστω και για κάποιο συγκεκριμένο  . Αν γνωρίζει κάποιος κάτι επ' αυτού, θα ήταν ενδιαφέρον να το μάθουμε.
. Αν γνωρίζει κάποιος κάτι επ' αυτού, θα ήταν ενδιαφέρον να το μάθουμε.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σύγκλιση ακολουθιών συναρτήσεων
Δημήτρη, αυτό είναι θαυμάσιο!
Αν και όποτε μπορέσεις, σε παρακαλώ, δώσε μας μια "σκιαγράφηση" των βημάτων εύρεσης.
Υ.Γ.1. Θα μπορούσαμε να τολμήσουμε έναν ανάλογο υπολογισμό για την γενική περίπτωση
 , -ίσως- με την βοήθεια της συνάρτησης Riemann ;
, -ίσως- με την βοήθεια της συνάρτησης Riemann ;Υ.Γ.2. Βέβαια, υπάρχει και η ακόμα γενικότερη περίπτωση
 ,
,
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Σύγκλιση ακολουθιών συναρτήσεων
Ναι Γρηγόρη. Με τη συνάρτηση ζήτα μπορούμε να τα βρούμε όλα. (Η εμφάνιση των  μας υποψιάζει για αυτό.) Έστω
μας υποψιάζει για αυτό.) Έστω  με
με  .
.
Ας παρατηρήσουμε αρχικά ότι

και

Ας παρατηρήσουμε τώρα ότι

όπου είναι το σύνολο όλων των
είναι το σύνολο όλων των  με
με  και
και  το σύνολο όλων των
το σύνολο όλων των  με
με  .
.
Έχουμε

και

Καταλήγουμε στο:

 μας υποψιάζει για αυτό.) Έστω
μας υποψιάζει για αυτό.) Έστω  με
με  .
.Ας παρατηρήσουμε αρχικά ότι

και

Ας παρατηρήσουμε τώρα ότι

όπου
 είναι το σύνολο όλων των
είναι το σύνολο όλων των  με
με  και
και  το σύνολο όλων των
το σύνολο όλων των  με
με  .
.Έχουμε

και

Καταλήγουμε στο:

Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 24 επισκέπτες