
μεταμεσονύκτιο ολοκλήρωμα 41
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
μεταμεσονύκτιο ολοκλήρωμα 41
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Λέξεις Κλειδιά:
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: μεταμεσονύκτιο ολοκλήρωμα 41
Σωστός και πάλι 
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: μεταμεσονύκτιο ολοκλήρωμα 41
Σχετικό ποστ υπάρχει εδώ.
Και κάτι πιο γενικό : (Frullani)
Έστω συνεχώς παραγωγίσιμη με
συνεχώς παραγωγίσιμη με  μονότονη στο
μονότονη στο  και
και 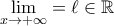 . Ας δειχθεί ότι για
. Ας δειχθεί ότι για 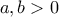 είναι
είναι
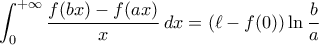 .
.
Και κάτι πιο γενικό : (Frullani)
Έστω
 συνεχώς παραγωγίσιμη με
συνεχώς παραγωγίσιμη με  μονότονη στο
μονότονη στο  και
και 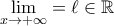 . Ας δειχθεί ότι για
. Ας δειχθεί ότι για 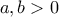 είναι
είναι 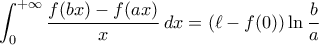 .
.Εσύ....; Θα γίνεις κανίβαλος....;
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot], MSN [Bot] και 22 επισκέπτες


 .
.