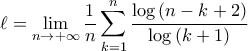
Ένα όριο
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
-
Δημοσθένης1043
- Δημοσιεύσεις: 47
- Εγγραφή: Τρί Δεκ 19, 2023 6:27 pm
Re: Ένα όριο
Rewriting gives
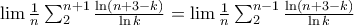 .
.First we get rid of the 3: we have
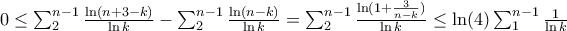 . This is
. This is 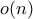 by SC hence we can forget the 3 and find
by SC hence we can forget the 3 and find 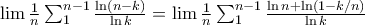 .
.Now we will show that we can forget about the second term within the summation.
Since
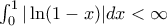 we have
we have 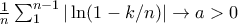 . One can prove this rigourously by noting that the Riemann sums are less than the integral. Hence we have some constant
. One can prove this rigourously by noting that the Riemann sums are less than the integral. Hence we have some constant  such that
such that 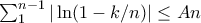 for all
for all  . Now fix
. Now fix 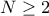 and let
and let 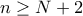 , then
, then 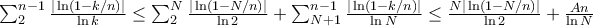 . Hence
. Hence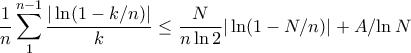 This implies
This implies 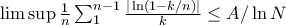 . Since
. Since  is arbitrary, we have
is arbitrary, we have 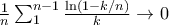 .
.Hence our limit simplifies to
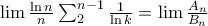 where
where 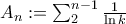 and
and 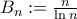 . We will try SC. We have
. We will try SC. We have 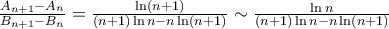 (quotient has limit 1), hence
(quotient has limit 1), hence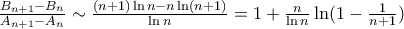 . This has limit 1, hence 1 is also the answer to the problem.
. This has limit 1, hence 1 is also the answer to the problem.-
Δημοσθένης1043
- Δημοσιεύσεις: 47
- Εγγραφή: Τρί Δεκ 19, 2023 6:27 pm
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ένα όριο
.
Γράφω λύση με δικά μου λόγια γιατί α) η μέθοδος του Δημοσθένη έχει πάρα πολλά περιττά περί το μέσον της απόδειξής του, κάνοντας τα εύκολα, δύσκολα και β) έχει ουσιατικό κενό δύο γραμμές πριν από το τέλος (αυτό που αφήνει είναι το ουσιαστικό μέρος της άσκησης).
Έχουμε
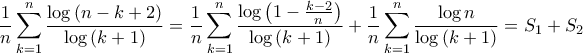 .
. α)
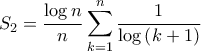 το οποίο είναι ασυμπτωτικό με το
το οποίο είναι ασυμπτωτικό με το 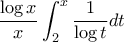 . To ολοκλήρωμα που εμφανίζεται είναι εξ ορισμού το
. To ολοκλήρωμα που εμφανίζεται είναι εξ ορισμού το 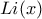 (βλέπε εδώ) και είναι γνωστό ότι ισχύει
(βλέπε εδώ) και είναι γνωστό ότι ισχύει 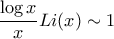 (υπάρχει, για παράδειγμα, περίπου στο μέσον της σελίδας στην παραπομπή που σημείωσα. Ακροβέστερα, το έχει για την
(υπάρχει, για παράδειγμα, περίπου στο μέσον της σελίδας στην παραπομπή που σημείωσα. Ακροβέστερα, το έχει για την 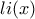 αλλά η
αλλά η 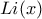 και η
και η 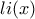 διαφέρουν κατά σταθερά). Συμπεραίνουμε ότι
διαφέρουν κατά σταθερά). Συμπεραίνουμε ότι 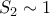 .
. Aν θέλουμε άλλη απόδειξη του ιδίου, μπορούμε να εργαστούμε με το θεώρημα Stolz (βλέπε εδώ) χρησιμοποιώντας τις μονότονες ακολουθίες
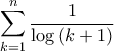 και
και 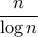 . Έχουμε τότε προς τον σκοπό αυτό
. Έχουμε τότε προς τον σκοπό αυτό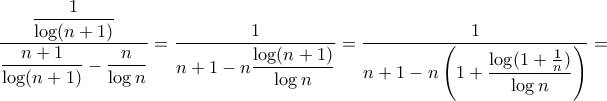
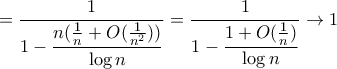 , που ολοκληρώνει την δεύτερη απόδειξη.
, που ολοκληρώνει την δεύτερη απόδειξη.β)
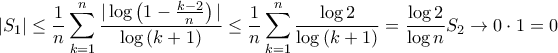
Τελικά, από τις α) και β), το ζητούμενο όριο ισούται με
 .
.- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ένα όριο
Μία προσέγγιση βασισμένη στις 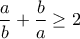 και
και 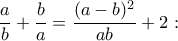
Χρησιμοποιώντας την βασική ανισότητα
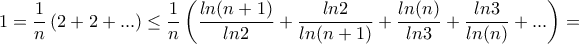
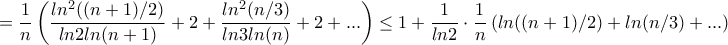
συμπεραίνουμε ότι αρκεί να δειχθεί η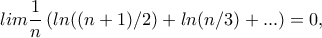
η οποία προκύπτει εύκολα από τις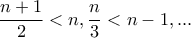 και την συνεπαγόμενη
και την συνεπαγόμενη
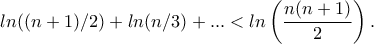
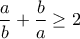 και
και 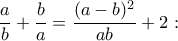
Χρησιμοποιώντας την βασική ανισότητα
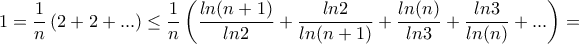
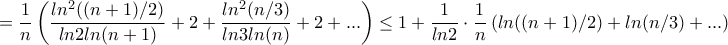
συμπεραίνουμε ότι αρκεί να δειχθεί η
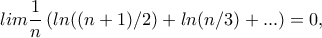
η οποία προκύπτει εύκολα από τις
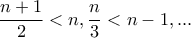 και την συνεπαγόμενη
και την συνεπαγόμενη 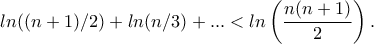
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ένα όριο
Πρωτοχρονιάτικη γκάφα στο τέλος, θα δω αν σώζεται, τώρα δεν ευκαιρώ
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ένα όριο
Δεν σώζεται με τίποτα η προσέγγιση μου, πέραν του τεράστιου λάθους στο τέλος υπήρχε και άλλο, καθώς το όριο που θα ήθελα να είναι
 ισούται τελικά προς
ισούται τελικά προς  (όπως μου δείχνει το λογισμικό)
(όπως μου δείχνει το λογισμικό) Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 3 επισκέπτες

