
μεταμεσονύκτιο ολοκλήρωμα 48
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
μεταμεσονύκτιο ολοκλήρωμα 48

Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Λέξεις Κλειδιά:
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: μεταμεσονύκτιο ολοκλήρωμα 48
Είναιmathxl έγραψε:
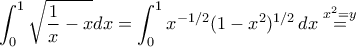



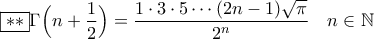
 .
.Η ολοκληρωτέα δεν έχει στοιχειώδη παράγουσα
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Παρ Ιουν 04, 2010 11:55 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
Re: μεταμεσονύκτιο ολοκλήρωμα 48
Έχουμε ακριβώς την ίδια λύση μόνο που σταμάτησα στο προτελευταίο "=" διότι δεν χρησιμοποίησα την σχέση ***Κοτρώνης Αναστάσιος έγραψε:Είναιmathxl έγραψε:
.
Η ολοκληρωτέα δεν έχει στοιχειώδη παράγουσα
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες


 ισχύει
ισχύει  .
.


