![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.Ζητείται η πιθανότητα οι αριθμοί αυτοί να είναι τα μήκη των πλευρών ενός τριγώνου.
Ευθύμης
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.Κώδικας: Επιλογή όλων
clc;clear all;
n = input('Enter the number of simulations: ');
is_triangle = 0;
cum_prob_is_triangle = zeros(1,n);
for ii = 1 : n
x = rand();
y = rand();
z = rand();
if x + y < z
is_triangle = is_triangle + 1;
elseif x + z < y
is_triangle = is_triangle + 1;
elseif y + z < x
is_triangle = is_triangle + 1;
end
cum_prob_is_triangle(ii) = is_triangle / ii;
end
p = is_triangle / n;
fprintf('Probability computed from simulation: %.5f\n',p);
xaxis = 1 : n;
figure;
plot(xaxis , cum_prob_is_triangle,'linewidth',2,'color',[0,0.7,0.9]);
hold on;plot([0 n],[1/2,1/2],'linewidth',2.5,'color','red');
axis([0 n 0 1]);
xlabel ('Number Of Simulations');
ylabel ('Cumulative Probability Of Getting A Triangle');
hold off;![a,b,c \in [0,1] a,b,c \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/eb8f6c1628622d73176b4a5f9cc18269.png) κοιτάμε τον πιο μεγάλο, έστω
κοιτάμε τον πιο μεγάλο, έστω  . Mε τα μήκη αυτά μπορούμε να φτιάξουμε τρίγωνο αν και μόνον αν
. Mε τα μήκη αυτά μπορούμε να φτιάξουμε τρίγωνο αν και μόνον αν  . Στο κατρεσιανό επίπεδο αυτό σημαίνει ότι το σημείο
. Στο κατρεσιανό επίπεδο αυτό σημαίνει ότι το σημείο  είναι στην γκρι περιοχή η οποία ορίζεται πάνω από την ευθεία
είναι στην γκρι περιοχή η οποία ορίζεται πάνω από την ευθεία  . Αντίστροφα, αν το
. Αντίστροφα, αν το  είναι στην λευκή περιοχή του τετραγώνου, τότε δεν φτιάχνουμε τρίγωνο. Αλλά η γκρι περιοχή είναι όσο η λευκή. Άρα η πιθανότητα να φτιάξουμε τρίγωνο είναι
είναι στην λευκή περιοχή του τετραγώνου, τότε δεν φτιάχνουμε τρίγωνο. Αλλά η γκρι περιοχή είναι όσο η λευκή. Άρα η πιθανότητα να φτιάξουμε τρίγωνο είναι  . Συμβαίνει το ίδιο για κάθε
. Συμβαίνει το ίδιο για κάθε ![a\in [0,\,1] a\in [0,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/007f95ed0ea87cac7d3b2cffce36e61f.png) , οπότε η πιθανότητα είνα τελικά
, οπότε η πιθανότητα είνα τελικά  .
. και
και  .
. , οπότε θα είναι
, οπότε θα είναι  , και αφού τα σύνολα
, και αφού τα σύνολα  είναι προφανώς μια διαμέριση του
είναι προφανώς μια διαμέριση του ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) (είναι
(είναι 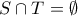 και
και ![S \cup T=[0,1] S \cup T=[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d3fcfdd7655fec89b9f5222b212c5ee0.png) ), έχουμε ότι η πιθανότητα μια τριάδα
), έχουμε ότι η πιθανότητα μια τριάδα  να ανήκει στο
να ανήκει στο  είναι
είναι  .
. , και WLOG
, και WLOG  . Τότε, ορίζουμε
. Τότε, ορίζουμε  . Είναι προφανώς
. Είναι προφανώς 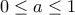 και
και  ,
, 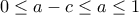 .
. , όπου η τελευταία ανισότητα ισχύει διότι
, όπου η τελευταία ανισότητα ισχύει διότι  . Άρα
. Άρα  . Αντίστροφα, έστω μία τριάδα
. Αντίστροφα, έστω μία τριάδα  όπου WLOG
όπου WLOG  , τότε προφανώς
, τότε προφανώς  .
. , συνεπώς η ζητούμενη πιθανότητα είναι πράγματι
, συνεπώς η ζητούμενη πιθανότητα είναι πράγματι  .
. να ισχύει
να ισχύει 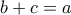 , καθώς τότε
, καθώς τότε  , οπότε τα
, οπότε τα  δεν σχηματίζουν τρίγωνο. Δηλαδή μας ενδιαφέρει η πιθανότητα μια τριάδα
δεν σχηματίζουν τρίγωνο. Δηλαδή μας ενδιαφέρει η πιθανότητα μια τριάδα  με τα
με τα ![a,b,c \in [0,1] a,b,c \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/eb8f6c1628622d73176b4a5f9cc18269.png) να ικανοποιεί την
να ικανοποιεί την 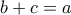 .
.  , τότε το πείραμα τύχης είναι η επιλογή δύο αριθμών
, τότε το πείραμα τύχης είναι η επιλογή δύο αριθμών  και
και  στο
στο  , ώστε
, ώστε 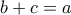 . Έστω λοιπόν η μεταβλητή
. Έστω λοιπόν η μεταβλητή  , και θέλουμε την
, και θέλουμε την  .
.  παίρνει τιμές στο
παίρνει τιμές στο ![[0,2a] [0,2a]](/forum/ext/geomar/texintegr/latexrender/pictures/9caa1c04c5b4af0f5b77e55dd2befcab.png) , επειδή
, επειδή  . Αφού όμως η μεταβλητή είναι συνεχής (το
. Αφού όμως η μεταβλητή είναι συνεχής (το ![[0,2a] [0,2a]](/forum/ext/geomar/texintegr/latexrender/pictures/9caa1c04c5b4af0f5b77e55dd2befcab.png) είναι υπεραριθμήσιμο), η πιθανότητα ισούται με
είναι υπεραριθμήσιμο), η πιθανότητα ισούται με  . Άρα δεν έχουμε πρόβλημα)
. Άρα δεν έχουμε πρόβλημα)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης