 ενός ημικυκλίου φέρουμε χορδή
ενός ημικυκλίου φέρουμε χορδή  παράλληλη προς τη διάμετρο
παράλληλη προς τη διάμετρο 
και την εφαπτομένη του τόξου , η οποία τέμνει την προέκταση της διαμέτρου στο σημείο
 .
.Βρείτε εκείνες τις θέσεις του
 για τις οποίες : α) Μεγιστοποιείται το
για τις οποίες : α) Μεγιστοποιείται το 
β) Είναι :
 ...... γ) Μεγιστοποιείται η γωνία
...... γ) Μεγιστοποιείται η γωνία 





 άρα αρκεί
άρα αρκεί 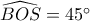
 και
και 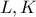 οι προβολές των
οι προβολές των 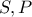 στη διάμετρο , θέτω:
στη διάμετρο , θέτω:  και θα ισχύουν :
και θα ισχύουν : 
 και αφού ως γνωστό τα σημεία
και αφού ως γνωστό τα σημεία  είναι
είναι  θα είναι :
θα είναι : 
 προκύπτει
προκύπτει  άρα
άρα  και
και  συνεπώς και τα
συνεπώς και τα  , επειδή στο
, επειδή στο  η συνάρτηση
η συνάρτηση  είναι γνήσια αύξουσα αρκεί να μελετήσουμε το λόγο
είναι γνήσια αύξουσα αρκεί να μελετήσουμε το λόγο  . Λόγω της
. Λόγω της  προκύπτει
προκύπτει  ενώ
ενώ  και εξ αιτίας της
και εξ αιτίας της  γίνονται
γίνονται  Έτσι
Έτσι  που
που  και μέγιστη τιμή
και μέγιστη τιμή  .
. και να φέρω το
και να φέρω το  .
. 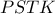 είναι παραλληλόγραμμο και
είναι παραλληλόγραμμο και 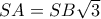 .
.