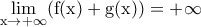 τότε για κάθε φυσικό
τότε για κάθε φυσικό  είναι
είναι
Συντονιστής: Παύλος Μαραγκουδάκης
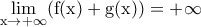 τότε για κάθε φυσικό
τότε για κάθε φυσικό  είναι
είναι
Με χρήση της Holder, στην ειδική περίπτωσηΠαύλος Μαραγκουδάκης έγραψε: ↑Σάβ Ιούλ 06, 2019 2:31 pmΝα αποδείξετε ότι αντότε για κάθε φυσικό
είναι

 , για
, για 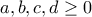 , με
, με 
 έχουμε με
έχουμε με 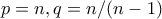
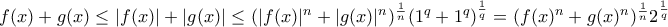 και το ζητούμενο έπεται από ισοσυγκλίνουσες.
και το ζητούμενο έπεται από ισοσυγκλίνουσες. όταν
όταν  μέσω τιμών με
μέσω τιμών με  . Μένει να εξετάσουμε τι γίνεται όταν
. Μένει να εξετάσουμε τι γίνεται όταν  μέσω τιμών από τα υπόλοιπα
μέσω τιμών από τα υπόλοιπα  . Εργαζόμαστε επαγωγικά. Για το επαγωγικό βήμα λέμε:
. Εργαζόμαστε επαγωγικά. Για το επαγωγικό βήμα λέμε:  , η παράσταση αυτή είναι θετική για μεγάλα
, η παράσταση αυτή είναι θετική για μεγάλα  . Χωρίς βλάβη
. Χωρίς βλάβη  , οπότε
, οπότε  . Επίσης από την επαγωγική υπόθεση είναι
. Επίσης από την επαγωγική υπόθεση είναι  για μεγάλα
για μεγάλα  . Έχουμε τότε
. Έχουμε τότε 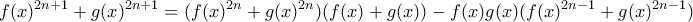
 , και λοιπά.
, και λοιπά. με
με 


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες