
να βρεθεί το μέγιστο της

2)Για

να βρεθεί το μέγιστο της

Συντονιστής: Παύλος Μαραγκουδάκης
Ας είναι
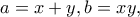 οπότε
οπότε 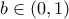 και
και 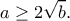


 οπότε εύκολα βλέπουμε ότι παρουσιάζει
οπότε εύκολα βλέπουμε ότι παρουσιάζει 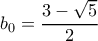 , το
, το 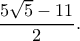
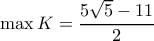 για
για 
Σωστά.
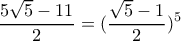
 με φυσιολογικό τρόπο.
με φυσιολογικό τρόπο.Για να δούμε την λύση.





 .
. .
. δίνει
δίνει (1)
(1) δίνει
δίνει (2)
(2)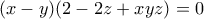


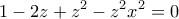
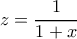
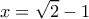

 !!!
!!!Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες