ΠΕΡΙ ΕΝΟΣ ΘΕΩΡΗΜΑΤΟΣ ΤΗΣ ΓΕΩΜΕΤΡΙΑΣ ΤΩΝ MORLEY-LEBESQUE του Θ. ΒΑΡΟΠΟΥΛΟΥ, ΠΡΑΚΤΙΚΑ ΑΚΑΔΗΜΙΑΣ ΑΘΗΝΩΝ

SKuruklis · #1

Πρόσφατα ο Ανδρέας Χατζηπολάκης εντόπισε στα Πρακτικά της Ακαδημίας, την ευρύτερα άγνωστη εργασία Περί ενός θεωρήματος της Γεωμετρίας των Morley – Lebesgue (Sur un theoreme de la geometrie de Morley – Lebesgue) του αείμνηστου καθηγητού στο ΑΠΘ Θ. Βαρόπουλου . Ίσως είναι η πρωταρχική εργασία της πλούσιας Ελληνικής συνεισφοράς στο θεώρημα Morley και αναμφίβολα κόσμημα της.

: Εργασία Βαρόπουλου.png (265.57 KiB) Προβλήθηκε 585 φορές

Η ανακοίνωση των περίπου 3 σελίδων, αρχικά διατυπώνει την πρόταση «αι εσωτερικοί τριχοτόμοι των γωνιών Α,Β,C, (πλησιέστερες προς τις πλευρές) τριγώνου τυχόντος ΑΒC, τεμνόμενες καθορίζουν ισόπλευρον τρίγωνο». Στη συνέχεια θέτει ως στόχο «τη γεωμετρική απόδειξη της ανωτέρω προτάσεως που έπεται από τα εξής γνωστά». Αυτά είναι 5 ισχυρισμοί που το ευρύτερο μαθηματικό κοινό μάλλον αγνοεί. Περιλαμβάνουν όρους όπως ευθύγραμμα τμήματα «εν εξέλιξιν» που ενώνουν τυχόν σημείο με τις κορυφές ενός πλήρους τετράπλευρου, συμμετρικό ευθυγράμμου τμήματος ως προς τρίγωνο, αντίστροφα σημεία ως προς τρίγωνο, ομόλογα τρίγωνα, ειδικά διαγράμματα. Στο τέλος παρατηρείται ότι με τον ίδιο τρόπο αποδεικνύεται το γενικό θεώρημα κατά το οποίο «οι τριχοτόμοι πλησιέστερες (προς μια πλευρά) του τριγώνου διαχωρίζονται 6 ανά 6 επί 9 ευθειών που είναι κορυφές 27 ισοπλεύρων τριγώνων».

Το κείμενο δεν αποτελεί εύκολο ανάγνωσμα. Απευθύνεται σε εξιδεικευμένο κοινό που μετά από εξηγήσεις και διευκρινήσεις εν τέλει θα πειστεί για την ορθότητα και πληρότητα της απόδειξης. Πέραν της μαθηματικής της αξίας η εργασία έχει ιστορικό ενδιαφέρον γιατί διαφωτίζει το λόγο που μετά από αυτήν γράφτηκαν στο ίδιο θέμα πληθώρα άλλες. Μεταξύ αυτών διακρίνονται για το γενικό θεώρημα η εργασία του Alain Connes με χρήση αυτομορφισμών Ομάδων (που δημιουργούνται από περιστροφές) και η μέθοδος εξωστρέφεια – extraversion του John Conway.

Η λακωνικότητα και απλότητα διατύπωσης του θεωρήματος Morley ικετεύει για μια σύντομη και στοιχειώδη τεκμηρίωση. Οι μαθηματικές αποδείξεις διακρίνονται για την ακρίβεια, σαφήνεια και διαύγεια στη ροή των ισχυρισμών που καταλήγουν στο αποδεικτέο. Επιπλέον κάθε θεώρημα έχει ιεραρχία. Για παράδειγμα η συνέχεια προηγείται της παραγώγου ή το θεώρημα των διαμέσων προηγείται του θεωρήματος Ceva. Η ιεραρχία των θεωρημάτων αποφεύγει περιττές επαναλήψεις, συμπυκνώνει τις αποδείξεις και διευκολύνει την κατανόηση τους.

Αναλύοντας τους όρους της διατύπωσης και διευκρινίζοντας ότι η τριχοτόμος πλησιέστερη προς πλευρά του τριγώνου είναι η τριχοτόμος που διχοτομεί τη γωνία μεταξύ της πλευράς και της άλλης τριχοτόμου, αναδεικνύεται ότι το θεώρημα Morley παρόλο που αναφέρεται σε τριχοτόμους βασίζεται εν τέλει σε ιδιότητες των διχοτόμων. Το δε γενικό θεώρημα προκύπτει από παραλλαγές του θεωρήματος των εσωτερικών τριχοτόμων για κατάλληλους συνδυασμούς ειδών τριχοτόμων.

Παρακάτω παρουσιάζεται μια πρόσφατη απόδειξη για το ειδικό θεώρημα που αξιοποιεί την παραπάνω θεμελιώδη παρατήρηση . Οι περιπτώσεις του γενικού θεωρήματος εμπεριέχονται σε αυτό το αρχείο.

ΑΠΟΔΕΙΞΗ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ MORLEY
Για την επαλήθευση του θεωρήματος δίδεται τρίγωνο $\triangle$ XYZ με μεγέθη γωνιών 3 $\alpha$ , 3 $\beta$ και 3 $\gamma$ , όπου $\alpha+\beta+\gamma=60^{0}$ . Θεωρούμε ότι οι τριχοτόμοι του $\triangle$ XYZ, πλησιέστερες στις πλευρές αντίστοιχα, τέμνονται στις κορυφές του $\triangle$ X'Y'Z', οπότε πρέπει να τεκμηριωθεί ότι το $\triangle$ X'Y'Z' είναι ισόπλευρο. Αυτό επιτυγχάνεται αν δειχθεί σε ένα άλλο $\triangle$ ABC το με ίσες τις αντίστοιχες γωνίες, δηλαδή τα $\triangle$ XYZ και $\triangle$ ABC είναι όμοια, ότι το αντίστοιχο $\triangle$ A'B'C' είναι ισόπλευρο. Η μέθοδος αυτή ονομάζεται πλάγια ή αντίστροφη και έχει χρησιμοποιηθεί και σε άλλες αποδείξεις του θεωρήματος.

Στη συνέχεια κατασκευάζεται το $\triangle$ ABC. Στο εξωτερικό ενός ισοπλεύρου $\triangle$ A'B'C' φτιάχνουμε ισοσκελή $\triangle$ B'A"C', $\triangle$ C'B"A' και $\triangle$ A'C"B' με γωνίες κορυφών $60^{0}+2\alpha$ , $60^{0}+2\beta$ και $60^{0}+2\gamma$ αντίστοιχα. Έτσι οι κορυφές του $\triangle$ ABC προκύπτουν από τις τομές αντίστοιχων πλευρών ισοσκελών τριγώνων.

: Κατασκευή του ΔABC από το ισόπλευρο ΔA'B'C' ώστε οι τριχοτόμοι του ΔABC, πλησιέστερες στις πλευρές, συναντώνται στις κορυφές του ΔA'B'C'.; Σχήμα1.png (173.33 KiB) Προβλήθηκε 585 φορές

Σύμφωνα με την παραπάνω περιγραφή της κατασκευής $\angle$ CA"B, $\angle$ AB"C και $\angle$ BC"A ταυτίζονται με τις αντίστοιχες γωνίες των κορυφών των ισοσκελών $\triangle$ C'A"B', $\triangle$ A'B"C' and $\triangle$ B'C"A', στα οποίες γωνίες οι A"A', B"B' και C"C' είναι διχοτόμοι αφού το $\triangle$ A'B'C' είναι ισόπλευρο.

Οι ίσες γωνίες των ισοσκελών έχουν μέγεθος 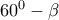$60^{0}-\alpha$ , $60^{0}-\beta$ και $60^{0}-\gamma$ αντίστοιχα. Έτσι
$\angle$ A'B'C $= \angle$ A'C'B $= 60^{0}+\alpha$ , $\angle$ B'C'A $=\angle$ B'A'C $= 60^{0}+\beta$ και $\angle$ C'A'B $=\angle$ C'B'A $=60^{0}+\gamma$ .
Άρα οι γωνίες μεταξύ των πλευρών των ισοσκελών που τεμνόμενες προσδιορίζουν τις κορυφές Α, Β και C,δηλαδή $\angle$ B'AC', $\angle$ C'BA' και $\angle$ A'CB', έχουν μεγέθη $\alpha$ , $\beta$ και $\gamma$ αντίστοιχα.

Όμως, όπως υποδεικνύει το παραπάνω σχήμα,
$\angle$ CA'B $= 360^{0} -(60^{0}+\gamma) - 60^{0} - (60^{0} +\beta)$ $=120^{0} + \alpha =$ $90^{0} + \frac{1}{2}\angle$ CA"B.

Αλλά όπως αποκαλύπτει το επόμενο σχήμα, το Α' είναι το έκκεντρο του $\triangle$ CA"B ως το μοναδικό σημείο της A"A', διχοτόμου της $\angle$ CA"B, από το οποία η πλευρά BC φαίνεται με γωνία αυτού του μεγέθους.

: Το έκκεντρο Ι και το παράκεντρο Ιz του ΔXYZ καθορίζονται από μια διχοτόμο και μια γωνία; Σχήμα2.png (51.58 KiB) Προβλήθηκε 585 φορές

Κυκλικά, τα B' και C' είναι έκκεντρα των $\triangle$ AB"C και $\triangle$ BC"A αντίστοιχα.

Καθώς τα B' και C' είναι έκκεντρα των $\triangle$ AB"C και $\triangle$ BC"A, η AC' διχοτομεί τη $\angle$ BAB' και η AB' διχοτομεί τη $\angle$ CAC'. Συνεπώς αυτές είναι τριχοτόμοι της $\angle$ CAB πλησιέστερες στις AB και AC αντίστοιχα. Επειδή $\angle$ C'AB'= $\alpha$ , $\angle$ CAB $= 3\alpha$ .
Κυκλικά οι BA' και BC' είναι τριχοτόμοι της $\angle$ ABC, πλησιέστερες στις AC και AB, ενώ CB' και CA' είναι τριχοτόμοι της $\angle$ BCA, πλησιέστερες στις CA και CB αντίστοιχα. Έτσι $\angle$ ABC $= 3\beta$ και $\angle$ BCA $= 3\gamma$ .
Επίσης οι κορυφές του $\triangle$ A'B'C' είναι τα σημεία τομής των τριχοτόμων του $\triangle$ ABC πλησιέστερων στις πλευρές. $\square$

ΠΕΡΙ ΕΝΟΣ ΘΕΩΡΗΜΑΤΟΣ ΤΗΣ ΓΕΩΜΕΤΡΙΑΣ ΤΩΝ MORLEY-LEBESQUE του Θ. ΒΑΡΟΠΟΥΛΟΥ, ΠΡΑΚΤΙΚΑ ΑΚΑΔΗΜΙΑΣ ΑΘΗΝΩΝ

ΠΕΡΙ ΕΝΟΣ ΘΕΩΡΗΜΑΤΟΣ ΤΗΣ ΓΕΩΜΕΤΡΙΑΣ ΤΩΝ MORLEY-LEBESQUE του Θ. ΒΑΡΟΠΟΥΛΟΥ, ΠΡΑΚΤΙΚΑ ΑΚΑΔΗΜΙΑΣ ΑΘΗΝΩΝ

Μέλη σε σύνδεση