 κινείται στην προέκταση της ακτίνας
κινείται στην προέκταση της ακτίνας  του τεταρτοκυκλίου
του τεταρτοκυκλίου  . Το τμήμα
. Το τμήμα 
τέμνει το τόξο στο σημείο
 . Βρείτε τον γεωμετρικό τόπο του μέσου
. Βρείτε τον γεωμετρικό τόπο του μέσου  , του τμήματος
, του τμήματος  .
.Συντονιστής: Παύλος Μαραγκουδάκης
 κινείται στην προέκταση της ακτίνας
κινείται στην προέκταση της ακτίνας  του τεταρτοκυκλίου
του τεταρτοκυκλίου  . Το τμήμα
. Το τμήμα 
 . Βρείτε τον γεωμετρικό τόπο του μέσου
. Βρείτε τον γεωμετρικό τόπο του μέσου  , του τμήματος
, του τμήματος  .
.Για ευκολία θέτω
 Με
Με  εύκολα βρίσκω
εύκολα βρίσκω  και
και  Αν
Αν  έχω
έχω  και
και  που είναι η εξίσωση του γεωμετρικού τόπου (η κόκκινη καμπύλη).
που είναι η εξίσωση του γεωμετρικού τόπου (η κόκκινη καμπύλη).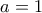 , οπότε
, οπότε  , άρα
, άρα 
 ,
, 

 οπότε έχουμε την εξίσωση
οπότε έχουμε την εξίσωση
 , με
, με  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης