Έστω ο μιγαδικός αριθμός
 του οποίου η εικόνα στο μιγαδικό επίπεδο βρίσκεται στον κύκλο
του οποίου η εικόνα στο μιγαδικό επίπεδο βρίσκεται στον κύκλο 
και η συνάρτηση

α. Να αποδείξετε ότι
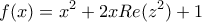
β. Αν
 για κάθε
για κάθε  :
:1. Να δείξετε ότι

2. Να βρεθεί το όριο
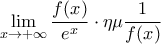
edit: Διόρθωση του τύπου της

Συντονιστής: m.pαpαgrigorakis
 του οποίου η εικόνα στο μιγαδικό επίπεδο βρίσκεται στον κύκλο
του οποίου η εικόνα στο μιγαδικό επίπεδο βρίσκεται στον κύκλο 

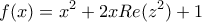
 για κάθε
για κάθε  :
:
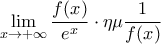


 .
. και για κάποιο λόγο δεν εμφανίζεται ο συζυγής στο δεύτερο z, μάλλον λόγω λάθος τύπου latex...Συγκεκριμένα χρησιμοποιούσα στην αρχική δημοσίευση την εντολή \overbar όπως φαίνεται εκεί για την εμφάνιση του συζυγούς, η οποία όμως δε λειτουργεί εδώ (μάλλον θα χρειάζεται ειδικό πακέτο latex)...
και για κάποιο λόγο δεν εμφανίζεται ο συζυγής στο δεύτερο z, μάλλον λόγω λάθος τύπου latex...Συγκεκριμένα χρησιμοποιούσα στην αρχική δημοσίευση την εντολή \overbar όπως φαίνεται εκεί για την εμφάνιση του συζυγούς, η οποία όμως δε λειτουργεί εδώ (μάλλον θα χρειάζεται ειδικό πακέτο latex)... οπότε τελικά
οπότε τελικά 
 Re(
Re(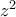 )+1
)+1 θα είναι και
θα είναι και  Re(
Re(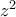 )+1
)+1 οπότε και
οπότε και  Re(
Re(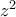 )
)  για
για 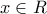 άρα Δ=
άρα Δ= ( Re(
( Re(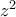 ))2
))2 επομένως θα είναι αναγκαία Re(
επομένως θα είναι αναγκαία Re(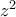 )=0 άρα
)=0 άρα 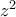 φανταστικός
φανταστικός το
το  και αν
και αν  επειδή
επειδή  και
και  το
το 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης