Για τις διάφορες τιμές του φυσικού
 να βρεθεί το όριο
να βρεθεί το όριο  όπου
όπου 
ΘΕΜΑ 2
Δίνεται η συνάρτηση
 με την ιδιότητα
με την ιδιότητα  για κάθε
για κάθε  Αν
Αν 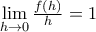 , να αποδείξετε ότι :
, να αποδείξετε ότι :α. η
 είναι συνεχής στο
είναι συνεχής στο  ,
, β. η
 είναι συνεχής στο
είναι συνεχής στο ,
,γ. Να βρείτε το
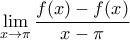 .
.ΘΕΜΑ3
Δίνεται η συνεχής συνάρτηση
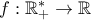 με την ιδιότητα
με την ιδιότητα 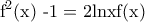 για κάθε
για κάθε .
.α. Να αποδείξετε ότι η συνάρτηση
 διατηρεί πρόσημο στο
διατηρεί πρόσημο στο 
β. Αν
 , τότε :
, τότε :i). να βρείτε το
 .
. ii). να βρείτε τον τύπο της

iii). να υπολογίσετε τα όρια
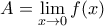 ,
, 
Α=
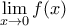 , Β=
, Β=
ΘΕΜΑ4
Δίνεται η συνεχής συνάρτηση
 με
με  και
και  για
για  .
. α. Να αποδείξετε ότι
 .
.β. Να αποδείξετε ότι υπάρχει
 ώστε
ώστε  .
. γ. Να υπολογίσετε το
 .
.δ. Να βρείτε το πρόσημο της
ε. Αν η
 είναι γνησίως μονότονη,
είναι γνησίως μονότονη, i) Nα βρείτε το είδος της μονοτονίας της
 .
. ii) Nα βρείτε το τύπο της
 .
.

 δίνει αμέσως
δίνει αμέσως  και το
και το  .
. το
το  και :
και :  ή
ή  ή
ή 
 θα είναι
θα είναι  .
. , άτοπο. Δεδομένου ότι είναι γνησίως μονότονη θα είναι γνησίως φθίνουσα.
, άτοπο. Δεδομένου ότι είναι γνησίως μονότονη θα είναι γνησίως φθίνουσα. . Θέτοντας τώρα
. Θέτοντας τώρα 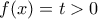 έχουμε τελικά
έχουμε τελικά  .
. , αλλά
, αλλά  που είναι τιμές της συνάρτησης, δηλαδή για τα
που είναι τιμές της συνάρτησης, δηλαδή για τα 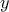 ώστε
ώστε 
![\displaystyle{ f(x) = \begin{cases} 6 & x \in [0,2) \\ 12/x & x \in [2,6] \\ 2 & x \in [6,+\infty) \end{cases}} \displaystyle{ f(x) = \begin{cases} 6 & x \in [0,2) \\ 12/x & x \in [2,6] \\ 2 & x \in [6,+\infty) \end{cases}}](/forum/ext/geomar/texintegr/latexrender/pictures/f0e9bb10a569b8c3f41e7a3c07710897.png)
 .
.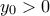 .
.  δίνει
δίνει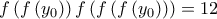 (1)
(1) :
: (2)
(2) 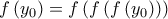
 , δηλαδή η συνάρτηση
, δηλαδή η συνάρτηση  . (Οεδ)
. (Οεδ) και εξισώνοντας πάλι τα
και εξισώνοντας πάλι τα  και χρησιμοποιώντας το ότι η συνάρτηση είναι γνησίως μονότονη άρα "1-1", προκύπτει ότι
και χρησιμοποιώντας το ότι η συνάρτηση είναι γνησίως μονότονη άρα "1-1", προκύπτει ότι  (3).
(3).  .
.