ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
Συντονιστής: KAKABASBASILEIOS
ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
Να συνεχίσουμε την προσπάθεια των συλλογών με Διαφορικό Λογισμό.
Παντούλας Περικλής
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
Μία απλή για αρχή
ΑΣΚΗΣΗ 71η
Η συνάρτηση είναι ορισμένη στο R, συνεχής στο σημείο
είναι ορισμένη στο R, συνεχής στο σημείο  και ισχύει
και ισχύει  . Να αποδείξετε ότι ισχύει
. Να αποδείξετε ότι ισχύει  .
.
ΑΣΚΗΣΗ 71η
Η συνάρτηση
 είναι ορισμένη στο R, συνεχής στο σημείο
είναι ορισμένη στο R, συνεχής στο σημείο  και ισχύει
και ισχύει  . Να αποδείξετε ότι ισχύει
. Να αποδείξετε ότι ισχύει  .
.Παντούλας Περικλής
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
Λύση άσκηση 71
Θεωρούμε τη συνάρτηση
 Θέτουμε
Θέτουμε  Συνεπώς
Συνεπώς  Έγινε αλλαγή ματαβλητής
Έγινε αλλαγή ματαβλητής 
Γιάννης
Θεωρούμε τη συνάρτηση
 Θέτουμε
Θέτουμε  Συνεπώς
Συνεπώς  Έγινε αλλαγή ματαβλητής
Έγινε αλλαγή ματαβλητής 
Γιάννης
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
- ΔΗΜΗΤΡΙΟΣ ΚΑΤΣΙΠΟΔΑΣ
- Δημοσιεύσεις: 681
- Εγγραφή: Δευ Απρ 20, 2009 8:25 pm
- Τοποθεσία: Καλαμάτα
- Επικοινωνία:
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΑΣΚΗΣΗ 72
Η συνάρτηση :
: είναι δύο φορές παραγωγίσιμη και ισχύουν οι σχέσεις
είναι δύο φορές παραγωγίσιμη και ισχύουν οι σχέσεις


 για κάθε
για κάθε 
α. Να δείξετε οτι
β. Να αποδείξετε οτι
γ. Να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της στο σημείο
στο σημείο 
δ. Να αποδείξετε οτι η εξίσωση δεν μπορεί να έχει δύο διαφορετικές ρίζες στο διάστημα
δεν μπορεί να έχει δύο διαφορετικές ρίζες στο διάστημα 
ε. Να αποδείξετε οτι υπάρχει τέτοιο ώστε
τέτοιο ώστε 
στ. Να αποδείξετε οτι υπάρχουν τέτοια ώστε
τέτοια ώστε 
Ι.Γαρατζιώτης & Π. Μάστακας (εκδόσεις Κέδρος)
Η συνάρτηση
 :
: είναι δύο φορές παραγωγίσιμη και ισχύουν οι σχέσεις
είναι δύο φορές παραγωγίσιμη και ισχύουν οι σχέσεις

 για κάθε
για κάθε 
α. Να δείξετε οτι

β. Να αποδείξετε οτι

γ. Να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της
 στο σημείο
στο σημείο 
δ. Να αποδείξετε οτι η εξίσωση
 δεν μπορεί να έχει δύο διαφορετικές ρίζες στο διάστημα
δεν μπορεί να έχει δύο διαφορετικές ρίζες στο διάστημα 
ε. Να αποδείξετε οτι υπάρχει
 τέτοιο ώστε
τέτοιο ώστε 
στ. Να αποδείξετε οτι υπάρχουν
 τέτοια ώστε
τέτοια ώστε 
Ι.Γαρατζιώτης & Π. Μάστακας (εκδόσεις Κέδρος)

Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
α) Στη σχέσηΔΗΜΗΤΡΙΟΣ ΚΑΤΣΙΠΟΔΑΣ έγραψε:ΑΣΚΗΣΗ 72
Η συνάρτηση:
είναι δύο φορές παραγωγίσιμη και ισχύουν οι σχέσεις
για κάθε
α. Να δείξετε οτι
β. Να αποδείξετε οτι
γ. Να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης τηςστο σημείο
δ. Να αποδείξετε οτι η εξίσωσηδεν μπορεί να έχει δύο διαφορετικές ρίζες στο διάστημα
ε. Να αποδείξετε οτι υπάρχειτέτοιο ώστε
στ. Να αποδείξετε οτι υπάρχουντέτοια ώστε
Ι.Γαρατζιώτης & Π. Μάστακας (εκδόσεις Κέδρος)
 θέτω
θέτω  με
με  . Τότε
. Τότε  και
και  .
. Αφού η
 συνεχής στο
συνεχής στο  (ως παραγωγίσιμη) έχουμε
(ως παραγωγίσιμη) έχουμε 
β)Έχουμε
 (Σχέση 1)
(Σχέση 1)Επιπλέον
 ( όπου
( όπου  ).
).Τότε στη σχέση 1 θέτω
 με
με  και
και  .
.Άρα
 .
. Οπότε

γ) Η εφαπτομένη της
 στο
στο  έχει εξίσωση
έχει εξίσωση 
δ) Έστω ότι η εξίσωση
 έχει δύο διαφορετικές ρίζες
έχει δύο διαφορετικές ρίζες  στο διάστημα
στο διάστημα  . Τότε
. Τότε  και επιπλέον η
και επιπλέον η  είναι συνεχής στο
είναι συνεχής στο ![\displaystyle{\left[ {\rho _1 ,\rho _2 } \right] \subset \left( {0,2} \right)} \displaystyle{\left[ {\rho _1 ,\rho _2 } \right] \subset \left( {0,2} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/4df7020a29d197fcc763a30153d6c85c.png) ως
ως παραγωγίσιμη (αφού η
 δύο φορές παραγωγίσιμη) και παραγωγίσιμη στο αντίστοιχο ανοιχτό διάστημα. Από θεώρημα
δύο φορές παραγωγίσιμη) και παραγωγίσιμη στο αντίστοιχο ανοιχτό διάστημα. Από θεώρημα  λοιπόν, θα υπάρχει
λοιπόν, θα υπάρχει  τέτοιο ώστε
τέτοιο ώστε . Άτοπο, αφού
. Άτοπο, αφού  για κάθε
για κάθε  . Συνεπώς η εξίσωση
. Συνεπώς η εξίσωση  δεν μπορεί να έχει δύο ρίζες στο
δεν μπορεί να έχει δύο ρίζες στο  .
.ε) Θεωρώ τη συνάρτηση
![\displaystyle{h\left( x \right) = f\left( x \right) - 2 + x,x \in \left[ {0,2} \right]} \displaystyle{h\left( x \right) = f\left( x \right) - 2 + x,x \in \left[ {0,2} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b63138e242a25e9769c308264dcbdd6a.png) . Η
. Η  συνεχής στο
συνεχής στο ![\displaystyle{\left[ {0,2} \right]
} \displaystyle{\left[ {0,2} \right]
}](/forum/ext/geomar/texintegr/latexrender/pictures/5786b599ca8feeaef15a8ca3ca27c220.png) αφού η
αφού η  συνεχής και επιπλέον
συνεχής και επιπλέον και
και .
. Από θεώρημα
 , υπάρχει
, υπάρχει  τέτοιο ώστε
τέτοιο ώστε 
στ) Η
 ικανοποιεί τις προϋποθέσεις του Θεωρήματος Μέσης Τιμής στα διαστήματα
ικανοποιεί τις προϋποθέσεις του Θεωρήματος Μέσης Τιμής στα διαστήματα ![\displaystyle{\left[ {0,\xi } \right]} \displaystyle{\left[ {0,\xi } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/f334573b871cbf2068662366a2f8d20a.png) και
και ![\displaystyle{\left[ {\xi ,2} \right]} \displaystyle{\left[ {\xi ,2} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/742daa8baeb350235af7247ab4f494e1.png) , όπου
, όπου  , το
, το  του ερωτήματος (ε) και συνεπώς υπάρχουν
του ερωτήματος (ε) και συνεπώς υπάρχουν και
και  τέτοια ώστε
τέτοια ώστε και
και .
. Οπότε

Παντούλας Περικλής
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΑΣΚΗΣΗ 73η
Έστω η συνάρτηση .
.
i) Να μελετηθεί η συνάρτηση ως προς την μονοτονία, τα ακρότατα, τα κοίλα και τα σημεία καμπής
ii) Να βρείτε το σύνολο τιμών της f
iii) Να δείξετε ότι
iv) Έστω η συνάρτηση για την οποία ισχύει ότι:
για την οποία ισχύει ότι:  . Να δείξετε ότι
. Να δείξετε ότι 
Edit: Μπαϊλάκης(εκδόσεις Σαββάλας)
Έστω η συνάρτηση
 .
.i) Να μελετηθεί η συνάρτηση ως προς την μονοτονία, τα ακρότατα, τα κοίλα και τα σημεία καμπής
ii) Να βρείτε το σύνολο τιμών της f
iii) Να δείξετε ότι

iv) Έστω η συνάρτηση
 για την οποία ισχύει ότι:
για την οποία ισχύει ότι:  . Να δείξετε ότι
. Να δείξετε ότι 
Edit: Μπαϊλάκης(εκδόσεις Σαββάλας)
Παντούλας Περικλής
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΛΥΣΗ ΑΣΚΗΣΗΣ 73
a) Είναι
Είναι , έτσι η
, έτσι η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![(-\infty,0] (-\infty,0]](/forum/ext/geomar/texintegr/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png) κσι γνησίως φθίνουσα στο
κσι γνησίως φθίνουσα στο 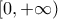 και παρουσιάζει ολικό μέγιστο για
και παρουσιάζει ολικό μέγιστο για  το
το 
Ακόμη
και
Έτσι η είναι κοίλη στο
είναι κοίλη στο ![(-\infty,3] (-\infty,3]](/forum/ext/geomar/texintegr/latexrender/pictures/79cff27b0ffd8687c8710cd78ac5defa.png) και κυρτή στο
και κυρτή στο  και παρουσιάζει καμπή στο σημείο
και παρουσιάζει καμπή στο σημείο 
β) Είναι![\Delta _{1}=(-\infty,0]\Rightarrow f(\Delta _{1})=(lim_{x\rightarrow -\infty}f(x),f(0)]=(-\infty,1] \Delta _{1}=(-\infty,0]\Rightarrow f(\Delta _{1})=(lim_{x\rightarrow -\infty}f(x),f(0)]=(-\infty,1]](/forum/ext/geomar/texintegr/latexrender/pictures/f8acee10aeb7b0fd5a0e0c17d3bdf220.png) γιατί η
γιατί η  είναι συνεχής και γνησίως αύξουσα στο
είναι συνεχής και γνησίως αύξουσα στο  και
και

και![\Delta _{2}=[0,+\infty)\Rightarrow f(\Delta _{2})=(lim_{x\rightarrow +\infty}f(x),f(0)]=(0,1] \Delta _{2}=[0,+\infty)\Rightarrow f(\Delta _{2})=(lim_{x\rightarrow +\infty}f(x),f(0)]=(0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e39cd8cff07f095891c7964cd11730d7.png)
γιατί η είναι συνεχής και γνησίως φθίνουσα στο
είναι συνεχής και γνησίως φθίνουσα στο  και
και

Άρα![f(R)=f(\Delta _{1})\bigcup{f(\Delta _{2}})=(-\infty,1] f(R)=f(\Delta _{1})\bigcup{f(\Delta _{2}})=(-\infty,1]](/forum/ext/geomar/texintegr/latexrender/pictures/4c6d45c24f48399732647cbd0b77144d.png)
γ) Η παρουσιάζει ολικό μέγιστο το
παρουσιάζει ολικό μέγιστο το  άρα και
άρα και

δ) Είναι ( από το (γ) ερώτημα):

και από κριτήριο παρεμβολής θα ισχύει (1)
(1)
Θέτω με
με 
και
και αφού , από κριτήριο παρεμβολής είναι και
, από κριτήριο παρεμβολής είναι και

a) Είναι

Είναι
 , έτσι η
, έτσι η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![(-\infty,0] (-\infty,0]](/forum/ext/geomar/texintegr/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png) κσι γνησίως φθίνουσα στο
κσι γνησίως φθίνουσα στο 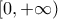 και παρουσιάζει ολικό μέγιστο για
και παρουσιάζει ολικό μέγιστο για  το
το 
Ακόμη

και

Έτσι η
 είναι κοίλη στο
είναι κοίλη στο ![(-\infty,3] (-\infty,3]](/forum/ext/geomar/texintegr/latexrender/pictures/79cff27b0ffd8687c8710cd78ac5defa.png) και κυρτή στο
και κυρτή στο  και παρουσιάζει καμπή στο σημείο
και παρουσιάζει καμπή στο σημείο 
β) Είναι
![\Delta _{1}=(-\infty,0]\Rightarrow f(\Delta _{1})=(lim_{x\rightarrow -\infty}f(x),f(0)]=(-\infty,1] \Delta _{1}=(-\infty,0]\Rightarrow f(\Delta _{1})=(lim_{x\rightarrow -\infty}f(x),f(0)]=(-\infty,1]](/forum/ext/geomar/texintegr/latexrender/pictures/f8acee10aeb7b0fd5a0e0c17d3bdf220.png) γιατί η
γιατί η  είναι συνεχής και γνησίως αύξουσα στο
είναι συνεχής και γνησίως αύξουσα στο  και
και 
και
![\Delta _{2}=[0,+\infty)\Rightarrow f(\Delta _{2})=(lim_{x\rightarrow +\infty}f(x),f(0)]=(0,1] \Delta _{2}=[0,+\infty)\Rightarrow f(\Delta _{2})=(lim_{x\rightarrow +\infty}f(x),f(0)]=(0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e39cd8cff07f095891c7964cd11730d7.png)
γιατί η
 είναι συνεχής και γνησίως φθίνουσα στο
είναι συνεχής και γνησίως φθίνουσα στο  και
και 
Άρα
![f(R)=f(\Delta _{1})\bigcup{f(\Delta _{2}})=(-\infty,1] f(R)=f(\Delta _{1})\bigcup{f(\Delta _{2}})=(-\infty,1]](/forum/ext/geomar/texintegr/latexrender/pictures/4c6d45c24f48399732647cbd0b77144d.png)
γ) Η
 παρουσιάζει ολικό μέγιστο το
παρουσιάζει ολικό μέγιστο το  άρα και
άρα και
δ) Είναι ( από το (γ) ερώτημα):

και από κριτήριο παρεμβολής θα ισχύει
 (1)
(1)Θέτω
 με
με 
και

και αφού
 , από κριτήριο παρεμβολής είναι και
, από κριτήριο παρεμβολής είναι και 
1. Δεν διδάσκουμε με αυτό που λέμε και κάνουμε. Διδάσκουμε με αυτό που είμαστε.
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΑΣΚΗΣΗ 74
Έστω 3 φορές παραγωγίσιμη συνάρτηση στο
3 φορές παραγωγίσιμη συνάρτηση στο  τέτοια ώστε να ισχύει
τέτοια ώστε να ισχύει  για κάθε
για κάθε  πραγματικό.
πραγματικό.
α) Να δείξετε ότι υπάρχει ένα τουλάχιστον τέτοιο ώστε
τέτοιο ώστε 
β) Να δείξετε ότι
γ) Να δείξετε ότι υπάρχει ένα τουλάχιστον τέτοιο ώστε
τέτοιο ώστε  .
.
(Τσακουμάγκος, Μπαλωμένου- Ελληνοεκδοτική)
Έστω
 3 φορές παραγωγίσιμη συνάρτηση στο
3 φορές παραγωγίσιμη συνάρτηση στο  τέτοια ώστε να ισχύει
τέτοια ώστε να ισχύει  για κάθε
για κάθε  πραγματικό.
πραγματικό.α) Να δείξετε ότι υπάρχει ένα τουλάχιστον
 τέτοιο ώστε
τέτοιο ώστε 
β) Να δείξετε ότι

γ) Να δείξετε ότι υπάρχει ένα τουλάχιστον
 τέτοιο ώστε
τέτοιο ώστε  .
.(Τσακουμάγκος, Μπαλωμένου- Ελληνοεκδοτική)
1. Δεν διδάσκουμε με αυτό που λέμε και κάνουμε. Διδάσκουμε με αυτό που είμαστε.
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
- ΔΗΜΗΤΡΙΟΣ ΚΑΤΣΙΠΟΔΑΣ
- Δημοσιεύσεις: 681
- Εγγραφή: Δευ Απρ 20, 2009 8:25 pm
- Τοποθεσία: Καλαμάτα
- Επικοινωνία:
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΛΥΣΗpito έγραψε:ΑΣΚΗΣΗ 74
Έστω3 φορές παραγωγίσιμη συνάρτηση στο
τέτοια ώστε να ισχύει
για κάθε
πραγματικό.
α) Να δείξετε ότι υπάρχει ένα τουλάχιστοντέτοιο ώστε
β) Να δείξετε ότι
γ) Να δείξετε ότι υπάρχει ένα τουλάχιστοντέτοιο ώστε
.
(Τσακουμάγκος, Μπαλωμένου- Ελληνοεκδοτική)
α.
Έχουμε

Για
 έχουμε
έχουμε 

Ενώ για
 έχουμε
έχουμε 

Από
 ,
,  έχουμε
έχουμε 
 συνεχής στο
συνεχής στο ![\displaystyle{[\alpha ,\beta ]} \displaystyle{[\alpha ,\beta ]}](/forum/ext/geomar/texintegr/latexrender/pictures/495a1910d13927c0bd1cea021aee0023.png) , διότι είναι παραγωγίσιμη στο
, διότι είναι παραγωγίσιμη στο 
 παραγωγίσιμη στο
παραγωγίσιμη στο  , διότι είναι παραγωγίσιμη στο
, διότι είναι παραγωγίσιμη στο 

Από θεώρημα
 υπάρχει ένα τουλάχιστον
υπάρχει ένα τουλάχιστον  τέτοιο ώστε
τέτοιο ώστε 
β.
Έχουμε
 ,
, 

Από την
 έχουμε οτι η
έχουμε οτι η  λαμβάνει μέγιστο στις θέσεις
λαμβάνει μέγιστο στις θέσεις  και
και  .
. Οπότε απο θεώρημα
 έχουμε
έχουμε 
γ.
 συνεχής στο
συνεχής στο ![\displaystyle{[\alpha ,x_1 ]} \displaystyle{[\alpha ,x_1 ]}](/forum/ext/geomar/texintegr/latexrender/pictures/ce90a146d8633f9e29a3313126969396.png) διότι είναι δυο φορές παραγωγίσιμη στο
διότι είναι δυο φορές παραγωγίσιμη στο 
 παραγωγίσιμη στο
παραγωγίσιμη στο  διότι είναι δυο φορες παραγωγίσιμη στο
διότι είναι δυο φορες παραγωγίσιμη στο 

Απο θεώρημα
 υπάρχει τουλάχιστον ένα
υπάρχει τουλάχιστον ένα  τέτοιο ώστε
τέτοιο ώστε 
 συνεχής στο
συνεχής στο ![\displaystyle{[x_1 ,\beta ]} \displaystyle{[x_1 ,\beta ]}](/forum/ext/geomar/texintegr/latexrender/pictures/64c105b24100f1abd983463bbef39fe5.png) διότι είναι δυο φορές παραγωγίσιμη στο
διότι είναι δυο φορές παραγωγίσιμη στο 
 παραγωγίσιμη στο
παραγωγίσιμη στο  διότι είναι δυο φορές παραγωγίσιμη στο
διότι είναι δυο φορές παραγωγίσιμη στο 

Απο θεώρημα
 υπάρχει τουλάχιστον ένα
υπάρχει τουλάχιστον ένα  τέτοιο ώστε
τέτοιο ώστε 
 συνεχής στο
συνεχής στο ![\displaystyle{[\xi _1 ,\xi _2 ]} \displaystyle{[\xi _1 ,\xi _2 ]}](/forum/ext/geomar/texintegr/latexrender/pictures/5a424563d55bcbf2d07e4a37e2c5c441.png) διότι είναι τρείς φορές παραγωγίσιμη στο
διότι είναι τρείς φορές παραγωγίσιμη στο 
 παραγωγίσιμη στο
παραγωγίσιμη στο  διότι είναι τρείς φορές παραγωγίσιμη στο
διότι είναι τρείς φορές παραγωγίσιμη στο 

Απο θεώρημα
 υπάρχει τουλάχιστον ένα
υπάρχει τουλάχιστον ένα  τέτοιο ώστε
τέτοιο ώστε 
τελευταία επεξεργασία από ΔΗΜΗΤΡΙΟΣ ΚΑΤΣΙΠΟΔΑΣ σε Πέμ Ιαν 19, 2012 8:58 am, έχει επεξεργασθεί 1 φορά συνολικά.

- ΔΗΜΗΤΡΙΟΣ ΚΑΤΣΙΠΟΔΑΣ
- Δημοσιεύσεις: 681
- Εγγραφή: Δευ Απρ 20, 2009 8:25 pm
- Τοποθεσία: Καλαμάτα
- Επικοινωνία:
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΑΣΚΗΣΗ 75
Έστω συνάρτηση δύο φορές παραγωγίσιμη στο
δύο φορές παραγωγίσιμη στο  με
με  , για κάθε
, για κάθε 
α. Να μελετηθεί η μονοτονία της
β. Να αποδείξετε οτι η αντιστρέφεται και να ορίσετε την
αντιστρέφεται και να ορίσετε την 
γ. Να βρεθεί το πρόσημο της
δ. Να αποδείξετε οτι η έχει ένα μόνο σημείο καμπής, το οποίο και να προσδιορίσετε
έχει ένα μόνο σημείο καμπής, το οποίο και να προσδιορίσετε
ε. Αν , να αποδείξετε οτι
, να αποδείξετε οτι 
στ. i. Να βρεθεί η μονοτονία της
ii. Να λυθεί η ανίσωση
Κ.Ρεκούμης & Κ.Λαγός (εκδόσεις Μεταίχμιο)
Έστω συνάρτηση
 δύο φορές παραγωγίσιμη στο
δύο φορές παραγωγίσιμη στο  με
με  , για κάθε
, για κάθε 
α. Να μελετηθεί η μονοτονία της

β. Να αποδείξετε οτι η
 αντιστρέφεται και να ορίσετε την
αντιστρέφεται και να ορίσετε την 
γ. Να βρεθεί το πρόσημο της

δ. Να αποδείξετε οτι η
 έχει ένα μόνο σημείο καμπής, το οποίο και να προσδιορίσετε
έχει ένα μόνο σημείο καμπής, το οποίο και να προσδιορίσετεε. Αν
 , να αποδείξετε οτι
, να αποδείξετε οτι 
στ. i. Να βρεθεί η μονοτονία της

ii. Να λυθεί η ανίσωση

Κ.Ρεκούμης & Κ.Λαγός (εκδόσεις Μεταίχμιο)

Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΛΥΣΗ ΑΣΚΗΣΗΣ 75
α) Είναι ( από παραγώγιση της δοσμένης )
και η είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  .
.
β) Η είναι
είναι  άρα και αντιστρέψιμη, αφού είναι γνησίως αύξουσα.
άρα και αντιστρέψιμη, αφού είναι γνησίως αύξουσα.
Θέτω στην δοσμένη, άρα
στην δοσμένη, άρα 
Το σύνολο τιμών της είναι το
είναι το  γιατί αν θέσω
γιατί αν θέσω  είναι και
είναι και

Άρα ή , ή
, ή  η οποία είναι αδύνατη γιατί
η οποία είναι αδύνατη γιατί  .
.
Έτσι λοιπόν
γ) Για στην αρχική είναι
στην αρχική είναι 
Για και αφού η
και αφού η  είναι γνησίως αύξουσα είναι
είναι γνησίως αύξουσα είναι 
και για και η
και η  έχει μοναδική ρίζα το 0.
έχει μοναδική ρίζα το 0.
δ) Αν παραγωγίσω 2 φορές την αρχική σχέση είναι .
.
Αν σημείο καμπής της
σημείο καμπής της  θα πρέπει
θα πρέπει  , αφού η
, αφού η  είναι 2 φορές παραγωγίσιμη.
είναι 2 φορές παραγωγίσιμη.
Έτσι για , γιατί αν είχα
, γιατί αν είχα
 , άτοπο΄.
, άτοπο΄.
Έτσι είναι αφού η
αφού η  είναι
είναι  .
.
Ακόμη για , άρα για
, άρα για  και αφού (από το (γ)) είναι
και αφού (από το (γ)) είναι 
θα είναι και και για
και για  θα είναι
θα είναι  .
.
Έτσι η θα είναι κοίλη στο
θα είναι κοίλη στο 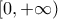 και κυρτή στο
και κυρτή στο ![(-\infty,0], f''(0)=0 (-\infty,0], f''(0)=0](/forum/ext/geomar/texintegr/latexrender/pictures/8edf7b10507879f016dbbbb9cca7c8cc.png) .
.
Άρα το είναι σημείο καμπής της
είναι σημείο καμπής της 
ε) Αρκεί να δείξω ότι (3)
(3)
Η είναι συνεχής στο
είναι συνεχής στο ![[0,a] [0,a]](/forum/ext/geomar/texintegr/latexrender/pictures/13596d6674a86fdafa24c4c414033e58.png) , παραγωγίσιμη στο
, παραγωγίσιμη στο  και από ΘΜΤ υπάρχει
και από ΘΜΤ υπάρχει
 και από ΘΜΤ στο
και από ΘΜΤ στο ![[a,\beta ] [a,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/b8c5d736aa7796891bcde958c2886f9b.png) ΄
΄
θα υπάρχει
Έτσι ( η
( η  είναι γνησίως
είναι γνησίως
φθίνουσα στο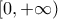 από το (δ) ερώτημα)
από το (δ) ερώτημα)
Η (4) ισχύει γιατί
ΣΤ) i) Είναι , όμως από το (α) είναι
, όμως από το (α) είναι  ΄
΄
διότι , που ισχύει.
, που ισχύει.
Έτσι και και η
και η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
ii) ,
,
αφού η είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Άρα τελικά
EDIT: Είχα ξεχάσει να βρω το σύνολο τιμών της . Ευχαριστώ τον κύριο Τηλέγραφο για την επισήμανση!
. Ευχαριστώ τον κύριο Τηλέγραφο για την επισήμανση!
α) Είναι ( από παραγώγιση της δοσμένης )

και η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  .
.β) Η
 είναι
είναι  άρα και αντιστρέψιμη, αφού είναι γνησίως αύξουσα.
άρα και αντιστρέψιμη, αφού είναι γνησίως αύξουσα.Θέτω
 στην δοσμένη, άρα
στην δοσμένη, άρα 
Το σύνολο τιμών της
 είναι το
είναι το  γιατί αν θέσω
γιατί αν θέσω  είναι και
είναι και 
Άρα ή
 , ή
, ή  η οποία είναι αδύνατη γιατί
η οποία είναι αδύνατη γιατί  .
.Έτσι λοιπόν

γ) Για
 στην αρχική είναι
στην αρχική είναι 
Για
 και αφού η
και αφού η  είναι γνησίως αύξουσα είναι
είναι γνησίως αύξουσα είναι 
και για
 και η
και η  έχει μοναδική ρίζα το 0.
έχει μοναδική ρίζα το 0.δ) Αν παραγωγίσω 2 φορές την αρχική σχέση είναι
 .
.Αν
 σημείο καμπής της
σημείο καμπής της  θα πρέπει
θα πρέπει  , αφού η
, αφού η  είναι 2 φορές παραγωγίσιμη.
είναι 2 φορές παραγωγίσιμη.Έτσι για
 , γιατί αν είχα
, γιατί αν είχα  , άτοπο΄.
, άτοπο΄.Έτσι είναι
 αφού η
αφού η  είναι
είναι  .
.Ακόμη για
 , άρα για
, άρα για  και αφού (από το (γ)) είναι
και αφού (από το (γ)) είναι 
θα είναι και
 και για
και για  θα είναι
θα είναι  .
.Έτσι η
 θα είναι κοίλη στο
θα είναι κοίλη στο 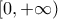 και κυρτή στο
και κυρτή στο ![(-\infty,0], f''(0)=0 (-\infty,0], f''(0)=0](/forum/ext/geomar/texintegr/latexrender/pictures/8edf7b10507879f016dbbbb9cca7c8cc.png) .
.Άρα το
 είναι σημείο καμπής της
είναι σημείο καμπής της 
ε) Αρκεί να δείξω ότι
 (3)
(3)Η
 είναι συνεχής στο
είναι συνεχής στο ![[0,a] [0,a]](/forum/ext/geomar/texintegr/latexrender/pictures/13596d6674a86fdafa24c4c414033e58.png) , παραγωγίσιμη στο
, παραγωγίσιμη στο  και από ΘΜΤ υπάρχει
και από ΘΜΤ υπάρχει και από ΘΜΤ στο
και από ΘΜΤ στο ![[a,\beta ] [a,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/b8c5d736aa7796891bcde958c2886f9b.png) ΄
΄θα υπάρχει

Έτσι
 ( η
( η  είναι γνησίως
είναι γνησίωςφθίνουσα στο
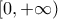 από το (δ) ερώτημα)
από το (δ) ερώτημα)Η (4) ισχύει γιατί

ΣΤ) i) Είναι
 , όμως από το (α) είναι
, όμως από το (α) είναι  ΄
΄διότι
 , που ισχύει.
, που ισχύει.Έτσι και
 και η
και η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
ii)
 ,
, αφού η
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Άρα τελικά

EDIT: Είχα ξεχάσει να βρω το σύνολο τιμών της
 . Ευχαριστώ τον κύριο Τηλέγραφο για την επισήμανση!
. Ευχαριστώ τον κύριο Τηλέγραφο για την επισήμανση!
τελευταία επεξεργασία από pito σε Πέμ Φεβ 09, 2012 12:00 pm, έχει επεξεργασθεί 1 φορά συνολικά.
1. Δεν διδάσκουμε με αυτό που λέμε και κάνουμε. Διδάσκουμε με αυτό που είμαστε.
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΑΣΚΗΣΗ 76
Δίνεται η παραγωγίσιμη συνάρτηση με την ιδιότητα
με την ιδιότητα 
για κάθε και
και  πραγματικό καθώς και
πραγματικό καθώς και  .
.
a) Να βρείτε την για
για  .
.
β) Να βρείτε την στο
στο  .
.
γ) Να βρείτε το ελάχιστο της .
.
δ) Να δείξετε ότι η είναι κυρτή στο
είναι κυρτή στο  και να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της
και να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της  στο σημείο
στο σημείο  .
.
ε) Αν για τους θετικούς πραγματικούς αριθμούς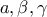 ισχύει
ισχύει  και
και  , να δείξετε ότι
, να δείξετε ότι  .
.
( Χρήστος Πατήλας, εκδόσεις Ελληνοεκδοτική)
Δίνεται η παραγωγίσιμη συνάρτηση
 με την ιδιότητα
με την ιδιότητα 
για κάθε
 και
και  πραγματικό καθώς και
πραγματικό καθώς και  .
.a) Να βρείτε την
 για
για  .
.β) Να βρείτε την
 στο
στο  .
.γ) Να βρείτε το ελάχιστο της
 .
.δ) Να δείξετε ότι η
 είναι κυρτή στο
είναι κυρτή στο  και να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της
και να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της  στο σημείο
στο σημείο  .
.ε) Αν για τους θετικούς πραγματικούς αριθμούς
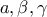 ισχύει
ισχύει  και
και  , να δείξετε ότι
, να δείξετε ότι  .
.( Χρήστος Πατήλας, εκδόσεις Ελληνοεκδοτική)
1. Δεν διδάσκουμε με αυτό που λέμε και κάνουμε. Διδάσκουμε με αυτό που είμαστε.
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
-
KAKABASBASILEIOS
- Συντονιστής
- Δημοσιεύσεις: 1598
- Εγγραφή: Κυρ Φεβ 01, 2009 1:46 pm
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
...στη χαρά της δημιουργίας...
ΑΣΚΗΣΗ 77
Έστω συνάρτηση που είναι συνεχής και γνήσια αύξουσα, για την οποία ισχύει ότι
που είναι συνεχής και γνήσια αύξουσα, για την οποία ισχύει ότι
 για κάθε
για κάθε 
α) Να δείξετε ότι για
για  και ότι
και ότι  .
.
β) Να δείξετε ότι η εξίσωση έχει τουλάχιστον μία ρίζα στο
έχει τουλάχιστον μία ρίζα στο  .
.
γ)Αν η είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  να βρεθεί η εξίσωση της εφαπτομένης της
να βρεθεί η εξίσωση της εφαπτομένης της  στο σημείο της
στο σημείο της  .
.
Φιλικά και Μαθηματικά
Βασίλης
ΑΣΚΗΣΗ 77
Έστω συνάρτηση
 που είναι συνεχής και γνήσια αύξουσα, για την οποία ισχύει ότι
που είναι συνεχής και γνήσια αύξουσα, για την οποία ισχύει ότι  για κάθε
για κάθε 
α) Να δείξετε ότι
 για
για  και ότι
και ότι  .
. β) Να δείξετε ότι η εξίσωση
 έχει τουλάχιστον μία ρίζα στο
έχει τουλάχιστον μία ρίζα στο  .
.γ)Αν η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  να βρεθεί η εξίσωση της εφαπτομένης της
να βρεθεί η εξίσωση της εφαπτομένης της  στο σημείο της
στο σημείο της  .
.Φιλικά και Μαθηματικά
Βασίλης
f ανοιγοντας τους δρομους της Μαθηματικης σκεψης, f' παραγωγος επιτυχιας
Τα Μαθηματικά είναι απλά...όταν σκέπτεσαι σωστά...
Τα Μαθηματικά είναι αυτά...για να δεις πιό μακρυά...
Τα Μαθηματικά είναι μαγεία...όταν έχεις φαντασία...
Τα Μαθηματικά είναι απλά...όταν σκέπτεσαι σωστά...
Τα Μαθηματικά είναι αυτά...για να δεις πιό μακρυά...
Τα Μαθηματικά είναι μαγεία...όταν έχεις φαντασία...
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
α)pito έγραψε:ΑΣΚΗΣΗ 76
Δίνεται η παραγωγίσιμη συνάρτησημε την ιδιότητα
για κάθεκαι
πραγματικό καθώς και
.
a) Να βρείτε τηνγια
.
β) Να βρείτε τηνστο
.
γ) Να βρείτε το ελάχιστο της.
δ) Να δείξετε ότι ηείναι κυρτή στο
και να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της
στο σημείο
.
ε) Αν για τους θετικούς πραγματικούς αριθμούςισχύει
και
, να δείξετε ότι
.
( Χρήστος Πατήλας, εκδόσεις Ελληνοεκδοτική)
Η δοθείσα για
 μιλώντας πάντα για θετικά
μιλώντας πάντα για θετικά  δίνει:
δίνει:
β)

και αφού
 είναι τελικά
είναι τελικά  και
και
γ)

Για
 είναι γνήσια αύξουσα και για
είναι γνήσια αύξουσα και για  είναι γνήσια φθίνουσα(πινακάκι κτλ.) και άρα ολικό ελάχιστο στο
είναι γνήσια φθίνουσα(πινακάκι κτλ.) και άρα ολικό ελάχιστο στο  το
το  .
.δ)
 άρα κυρτή!
άρα κυρτή!Η εφαπτομένη:

ε)

Η ισότητα ισχύει μόνο στο σημείο επαφής άρα θα πρεπε:
 που είναι αδύνατο λόγω του αθροίσματος των τριών άρα:
που είναι αδύνατο λόγω του αθροίσματος των τριών άρα: .
.Στραγάλης Χρήστος
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
Μία βραδυνή, για να τη βρουν οι πρωινοί 
ΑΣΚΗΣΗ 78η
Έστω οι συναρτήσεις , όπου η f είναι παραγωγίσιμη, με
, όπου η f είναι παραγωγίσιμη, με  και
και  , ώστε να ισχύει:
, ώστε να ισχύει:  , για κάθε
, για κάθε 
α) Να αποδείξετε ότι η συνάρτηση ικανοποιεί τις προϋποθέσεις του θεωρήματος Rolle στο διάστημα
ικανοποιεί τις προϋποθέσεις του θεωρήματος Rolle στο διάστημα ![\displaystyle{\left[ {1,e} \right]} \displaystyle{\left[ {1,e} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/5762a7e1a1745957664fcea68d4b01d2.png)
β) Να αποδείξετε ότι υπάρχει ξ, ώστε
γ) Να βρείτε την σταθερά
δ) Να βρείτε τον τύπο της συνάρτησης
Μπαϊλάκης- Εκδόσεις Σαβάλλα
ΑΣΚΗΣΗ 78η
Έστω οι συναρτήσεις
 , όπου η f είναι παραγωγίσιμη, με
, όπου η f είναι παραγωγίσιμη, με  και
και  , ώστε να ισχύει:
, ώστε να ισχύει:  , για κάθε
, για κάθε 
α) Να αποδείξετε ότι η συνάρτηση
 ικανοποιεί τις προϋποθέσεις του θεωρήματος Rolle στο διάστημα
ικανοποιεί τις προϋποθέσεις του θεωρήματος Rolle στο διάστημα ![\displaystyle{\left[ {1,e} \right]} \displaystyle{\left[ {1,e} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/5762a7e1a1745957664fcea68d4b01d2.png)
β) Να αποδείξετε ότι υπάρχει ξ, ώστε

γ) Να βρείτε την σταθερά

δ) Να βρείτε τον τύπο της συνάρτησης

Μπαϊλάκης- Εκδόσεις Σαβάλλα
Παντούλας Περικλής
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
1. συνεχής και παραγωγίσιμη στο
συνεχής και παραγωγίσιμη στο ![\displaystyle{[1,e]} \displaystyle{[1,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/e45e9c214f89168d99bc56eea3406327.png) ως πράξεις συνεχών και παρσγωγισίμων
ως πράξεις συνεχών και παρσγωγισίμων

υπάρχει
2. άρα
άρα 
3. οπότε
οπότε  αφου
αφου 
4.Από το 3ο έχουμε ή
ή  και επειδή
και επειδή  παίρνουμε
παίρνουμε 
εκανα μια μικρή διόρθωση της αρχικής συνθήκης f(1)=-1
 συνεχής και παραγωγίσιμη στο
συνεχής και παραγωγίσιμη στο ![\displaystyle{[1,e]} \displaystyle{[1,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/e45e9c214f89168d99bc56eea3406327.png) ως πράξεις συνεχών και παρσγωγισίμων
ως πράξεις συνεχών και παρσγωγισίμων
υπάρχει

2.
 άρα
άρα 
3.
 οπότε
οπότε  αφου
αφου 
4.Από το 3ο έχουμε
 ή
ή  και επειδή
και επειδή  παίρνουμε
παίρνουμε 
εκανα μια μικρή διόρθωση της αρχικής συνθήκης f(1)=-1
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
άσκηση 78
Έστελνα τη λύση της άσκησης αλλά την αποσύρω γιατί με πρόλαβε άλλος συνάδελφος βρήκα τη συνάρτηση
φιλικά
Γιάννης
Έστελνα τη λύση της άσκησης αλλά την αποσύρω γιατί με πρόλαβε άλλος συνάδελφος βρήκα τη συνάρτηση

φιλικά
Γιάννης
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
Στο ερώτημα δ είναι 
Γιάννης

Γιάννης
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
- ΔΗΜΗΤΡΙΟΣ ΚΑΤΣΙΠΟΔΑΣ
- Δημοσιεύσεις: 681
- Εγγραφή: Δευ Απρ 20, 2009 8:25 pm
- Τοποθεσία: Καλαμάτα
- Επικοινωνία:
Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
ΑΣΚΗΣΗ 79η
Δίνεται η συνάρτηση
α. Να μελετήσετε την συνάρτηση ως προς την μονοτονία και τα ακρότατα
ως προς την μονοτονία και τα ακρότατα
β. Να μελετήσετε την συνάρτηση ως προς την κυρτότητα
ως προς την κυρτότητα
γ. Να βρείτε το σύνολο τιμών της
δ. Να βρείτε το πλήθος των ριζών της εξίσωσης , για τις διάφορες τιμές του
, για τις διάφορες τιμές του 
ε. Να βρείτε το όριο
Α.Μπάρλας (εκδόσεις Ελληνοεκδοτική)
Δίνεται η συνάρτηση

α. Να μελετήσετε την συνάρτηση
 ως προς την μονοτονία και τα ακρότατα
ως προς την μονοτονία και τα ακρόταταβ. Να μελετήσετε την συνάρτηση
 ως προς την κυρτότητα
ως προς την κυρτότηταγ. Να βρείτε το σύνολο τιμών της

δ. Να βρείτε το πλήθος των ριζών της εξίσωσης
 , για τις διάφορες τιμές του
, για τις διάφορες τιμές του 
ε. Να βρείτε το όριο

Α.Μπάρλας (εκδόσεις Ελληνοεκδοτική)

Re: ΣΥΛΛΟΓΗ ΘΕΜΑΤΩΝ ΣΤΟ ΔΙΑΦΟΡΙΚΟ ΛΟΓΙΣΜΟ
Άσκηση 80
Αν μια συνάρτηση f είναι παραγωγίσιμη στο R και ικανοποιεί τη συνθήκη τότε
τότε
α. Να βρείτε τον τύπο της συνάρτησης
β. Να μελετήσετε την ως προς τη μονοτονία και τα κοίλα -κυρτά
ως προς τη μονοτονία και τα κοίλα -κυρτά
γ. Να βρείτε τα ακρότατα και τα σημεία καμπής
(Από το βιβλίο Γεώργιος Κομπότης Θεματογραφία Μαθηματικών Γ Λυκείου)
Γιάννης Σταματογιάννης
Αν μια συνάρτηση f είναι παραγωγίσιμη στο R και ικανοποιεί τη συνθήκη
 τότε
τότεα. Να βρείτε τον τύπο της συνάρτησης

β. Να μελετήσετε την
 ως προς τη μονοτονία και τα κοίλα -κυρτά
ως προς τη μονοτονία και τα κοίλα -κυρτά γ. Να βρείτε τα ακρότατα και τα σημεία καμπής
(Από το βιβλίο Γεώργιος Κομπότης Θεματογραφία Μαθηματικών Γ Λυκείου)
Γιάννης Σταματογιάννης
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
