 του περιγεγραμμένου κύκλου τριγώνου
του περιγεγραμμένου κύκλου τριγώνου 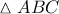 , το έγκεντρο του
, το έγκεντρο του  και το ορθόκεντρο
και το ορθόκεντρο  του τριγώνου με κορυφές
του τριγώνου με κορυφές τα σημεία επαφής του έγκυκλου του
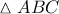 με τις πλευρές του είναι σημεία συνευθειακά.
με τις πλευρές του είναι σημεία συνευθειακά.Στάθης
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 του περιγεγραμμένου κύκλου τριγώνου
του περιγεγραμμένου κύκλου τριγώνου 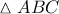 , το έγκεντρο του
, το έγκεντρο του  και το ορθόκεντρο
και το ορθόκεντρο  του τριγώνου με κορυφές
του τριγώνου με κορυφές 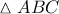 με τις πλευρές του είναι σημεία συνευθειακά.
με τις πλευρές του είναι σημεία συνευθειακά. με ορθόκεντρο
με ορθόκεντρο  και περίκεντρο
και περίκεντρο  ισχύει
ισχύει 
 και
και  το έκκεντρό του. Αν
το έκκεντρό του. Αν  είναι τα μέσα των κυρτογώνιων τόξων
είναι τα μέσα των κυρτογώνιων τόξων 
 είναι το ορθόκεντρο του
είναι το ορθόκεντρο του  .
. ισχύει:
ισχύει:  .
. ισχύει λόγω του Λήμματος 1 και 2:
ισχύει λόγω του Λήμματος 1 και 2: 
 .
.  είναι ομοιόθετα με λόγο
είναι ομοιόθετα με λόγο  και θα ισχύει για τα ομόλογα στοιχεία τους
και θα ισχύει για τα ομόλογα στοιχεία τους .
. .
. συνεπάγεται την συνευθειακότητα των
συνεπάγεται την συνευθειακότητα των  .
.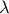 των
των  μπορεί και να εκφραστεί ως
μπορεί και να εκφραστεί ως 
 η ακτίνα του περιγεγραμμένου κύκλου και του εγγεγραμμένου κύκλου αντίστοιχα.
η ακτίνα του περιγεγραμμένου κύκλου και του εγγεγραμμένου κύκλου αντίστοιχα. είναι διχοτόμοι του τριγώνου
είναι διχοτόμοι του τριγώνου  . Επειδή
. Επειδή  είναι εφαπτόμενες του εγγεγραμμένου κύκλου,θα είναι
είναι εφαπτόμενες του εγγεγραμμένου κύκλου,θα είναι 
 στα
στα  οι οποίες ανά δύο τέμνονται στα
οι οποίες ανά δύο τέμνονται στα  .Έτσι ,στο τρίγωνο
.Έτσι ,στο τρίγωνο  τα
τα  είναι ύψη του και το
είναι ύψη του και το  είναι το ορθόκεντρό του .Επίσης θα είναι
είναι το ορθόκεντρό του .Επίσης θα είναι  κι έτσι υπάρχει ομοιοθεσία στην οποία τα τρίγωνα
κι έτσι υπάρχει ομοιοθεσία στην οποία τα τρίγωνα  είναι ομοιόθετα.Αυτό βέβαια συνεπάγεται ότι θα είναι ομοιόθετα και τα περίκεντρά τους και τα ορθόκεντρά τους.
είναι ομοιόθετα.Αυτό βέβαια συνεπάγεται ότι θα είναι ομοιόθετα και τα περίκεντρά τους και τα ορθόκεντρά τους. περνά από τους πόδες
περνά από τους πόδες των υψών του τριγώνου
των υψών του τριγώνου  και είναι μοναδικός που διέρχεται από τα σημεία αυτά,αυτός θα είναι ο κύκλος EULER του τριγώνου
και είναι μοναδικός που διέρχεται από τα σημεία αυτά,αυτός θα είναι ο κύκλος EULER του τριγώνου  .Έστω
.Έστω  το περίκεντρο του τριγώνου
το περίκεντρο του τριγώνου  .Γνωρίζουμε ότι το κέντρο
.Γνωρίζουμε ότι το κέντρο  του κύκλου EULER του τριγώνου
του κύκλου EULER του τριγώνου  βρίσκεται επί της
βρίσκεται επί της  που είναι η ευθεία EULER του τριγώνου
που είναι η ευθεία EULER του τριγώνου  και μάλιστα στο μέσον της.
και μάλιστα στο μέσον της. που αναφέραμε,το
που αναφέραμε,το  (περίκεντρο του τριγώνου
(περίκεντρο του τριγώνου  ) είναι ομοιόθετο του
) είναι ομοιόθετο του  (περίκεντρο του τριγώνου
(περίκεντρο του τριγώνου  ) και το
) και το 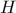 (ορθόκεντρο του τριγώνου
(ορθόκεντρο του τριγώνου  )είναι ομοιόθετο του
)είναι ομοιόθετο του  (ορθόκεντρο του τριγώνου
(ορθόκεντρο του τριγώνου  )Συνεπώς η ομοιόθετη της ευθείας EULER
)Συνεπώς η ομοιόθετη της ευθείας EULER  του τριγώνου
του τριγώνου  είναι η ευθεία EULER
είναι η ευθεία EULER  του τριγώνου
του τριγώνου 
 είναι σημείο της
είναι σημείο της  θα ανήκει και στην
θα ανήκει και στην  κι έτσι τα
κι έτσι τα  είναι συνευθειακά
είναι συνευθειακά ξέρουμε πως περνά από το μέσον του
ξέρουμε πως περνά από το μέσον του  οπότε
οπότε  .Όμως τα τρίγωνα
.Όμως τα τρίγωνα  είναι ορθογώνια με κοινή υποτείνουσα
είναι ορθογώνια με κοινή υποτείνουσα  κι έτσι
κι έτσι  .Αλλά και
.Αλλά και  οπότε η
οπότε η  είναι μεσοκάθετη της
είναι μεσοκάθετη της  Ακόμη
Ακόμη  Άρα
Άρα  . Επειδή
. Επειδή  ,και
,και  είναι
είναι 

 είναι όμοια οπότε
είναι όμοια οπότε  και αν
και αν ![\displaystyle{R,r}] \displaystyle{R,r}]](/forum/ext/geomar/texintegr/latexrender/pictures/13c6d249f1f85410fd707d84af3789e1.png) οι ακτίνες του περιγεγραμμένου-εγγεγραμμένου κύκλου του τριγώνου αντίστοιχα θα είναι
οι ακτίνες του περιγεγραμμένου-εγγεγραμμένου κύκλου του τριγώνου αντίστοιχα θα είναι 
 έχουμε
έχουμε 
![\[HI,OI] \[HI,OI]](/forum/ext/geomar/texintegr/latexrender/pictures/199d697138c4991b128fc5ac7a0c01dc.png) συναρτήσει των
συναρτήσει των ![\[R,r] \[R,r]](/forum/ext/geomar/texintegr/latexrender/pictures/89075186dea6872fe4453947811bd3a7.png)
 το μέσο του μικρού τόξου
το μέσο του μικρού τόξου  και
και  το σημείο τομής της
το σημείο τομής της  με την
με την  .
. 
 να είναι παράλληλες σαν κάθετες στην ίδια ευθεία, καταλήγοντας έτσι στην απάντηση.
να είναι παράλληλες σαν κάθετες στην ίδια ευθεία, καταλήγοντας έτσι στην απάντηση. , που είναι γνωστή πρόταση και αποδεικνύεται απλά.
, που είναι γνωστή πρόταση και αποδεικνύεται απλά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες