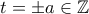και
και  . Να δειχτεί ότι οι αριθμοί
. Να δειχτεί ότι οι αριθμοί  είναι φυσικοί.
είναι φυσικοί.2. Έστω ορθογώνιο
 με
με 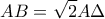 . Με διάμετρο την
. Με διάμετρο την  γράφουμε ημικύκλιο στο εξωτερικό του
γράφουμε ημικύκλιο στο εξωτερικό του  και συνδέουμε τυχαίο σημείο
και συνδέουμε τυχαίο σημείο  του ημικυκλίου με τα
του ημικυκλίου με τα  . Έστω
. Έστω 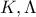 οι τομές των
οι τομές των 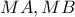 με την
με την  . Να δειχτεί ότι
. Να δειχτεί ότι 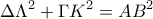 .
.(Η άσκηση αυτή κατασκευάστηκε από τον P. Fermat και λύσεις έδωσαν οι L.Euler, R.Simson κ.α.)
3. Να δειχτεί ότι ο αριθμός
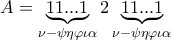 είναι σύνθετος για κάθε
είναι σύνθετος για κάθε  .
.4. Έστω
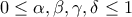 και
και 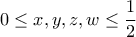 ώστε
ώστε 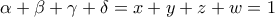 .
.Να δειχτεί ότι
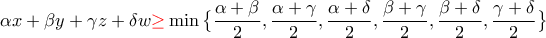 .
.edit
Αλλαγή φοράς από
 σε
σε  στo ζητούμενο του 4ου
στo ζητούμενο του 4ου
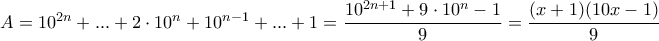 όπου
όπου 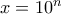 .Όμως είναι
.Όμως είναι 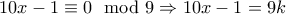 .Άρα
.Άρα 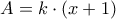 .
. και
και 

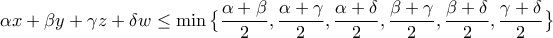 .
.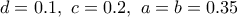 και
και 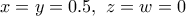
 για χάρη τυπογραφικής ευκολίας αλλά ισχύει για όλα τα
για χάρη τυπογραφικής ευκολίας αλλά ισχύει για όλα τα  )
)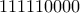 +
+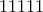
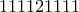
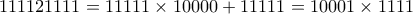
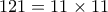
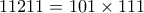
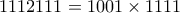
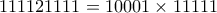
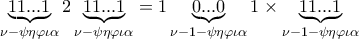
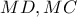 και τα κατακόρυφα τμήματα
και τα κατακόρυφα τμήματα 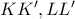 . Εύκολα από τα προκύπτοντα
. Εύκολα από τα προκύπτοντα 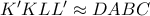 και
και 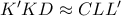 . Η πρώτη ομοιότητα δίνει :
. Η πρώτη ομοιότητα δίνει : 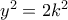 , ενώ η δεύτερη :
, ενώ η δεύτερη : 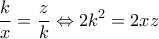 .
.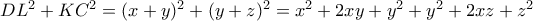
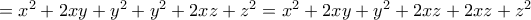
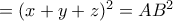
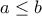 οι μικρότεροι από τους
οι μικρότεροι από τους 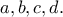 Τότε αρκεί να είναι:
Τότε αρκεί να είναι: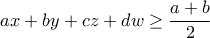 ή
ή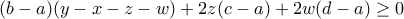
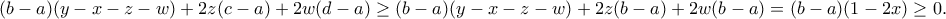
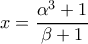 και
και 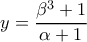
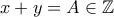 . Επίσης,
. Επίσης, 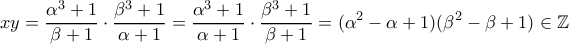 αφού
αφού 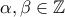 .
. είναι ρητοί. Επίσης είναι ρίζες του δευτεροβάθμιου πολυωνύμου
είναι ρητοί. Επίσης είναι ρίζες του δευτεροβάθμιου πολυωνύμου 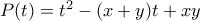 η οποία έχει ακέραιους συντελεστές. Επειδή ο συντελεστής του
η οποία έχει ακέραιους συντελεστές. Επειδή ο συντελεστής του 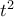 ισούται με
ισούται με  από το θεώρημα ρητής ρίζας κάθε ρητή ρίζα του
από το θεώρημα ρητής ρίζας κάθε ρητή ρίζα του 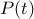 είναι ακέραια. Άρα τα
είναι ακέραια. Άρα τα 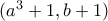 και ο
και ο 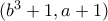 , αφού οι ρίζες που τεστάρουμε με το θεώρημα πρέπει να είναι σε ανάγωγη μορφή;
, αφού οι ρίζες που τεστάρουμε με το θεώρημα πρέπει να είναι σε ανάγωγη μορφή;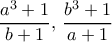 αλλά σε εξίσωση της μορφής
αλλά σε εξίσωση της μορφής 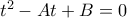 όπου τα
όπου τα  ξέρουμε ότι είναι ακέραιοι (συγκεκριμένα
ξέρουμε ότι είναι ακέραιοι (συγκεκριμένα  ) .
) . ακέραιοι τότε κάθε ρητή ρίζα, αν υπάρχει, της
ακέραιοι τότε κάθε ρητή ρίζα, αν υπάρχει, της 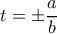 , όπου
, όπου 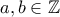 ,
, 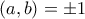 και
και 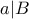 και
και 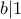 . Επομένως,
. Επομένως, 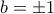 και άρα
και άρα