Ανάλυση,Θεωρητική - Όχι για μαθητές
Συντονιστής: emouroukos
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Ανάλυση,Θεωρητική - Όχι για μαθητές
Αν μια συνάρτηση f είναι γνησίως μονότονη στο IR και έχει σύνολο τιμών το IR , τότε η f είναι συνεχής.
Σχόλιο
Μπορεί άραγε να βρεθεί λύση που να εμπίπτει της σχολικής ύλης για αυτό το πρόβλημα ; Μου είπε ένας μαθητής ότι έκανε λύση, αλλά δεν τον ρώτησα πώς την έλυσε και σε τι βασίστηκε. Ακόμα όμως και η χρήση της άρνησης του ορισμού της συνέχειας είναι δύσκολη υπόθεση!
Σχόλιο
Μπορεί άραγε να βρεθεί λύση που να εμπίπτει της σχολικής ύλης για αυτό το πρόβλημα ; Μου είπε ένας μαθητής ότι έκανε λύση, αλλά δεν τον ρώτησα πώς την έλυσε και σε τι βασίστηκε. Ακόμα όμως και η χρήση της άρνησης του ορισμού της συνέχειας είναι δύσκολη υπόθεση!
- chris_gatos
- Επιμελητής
- Δημοσιεύσεις: 6962
- Εγγραφή: Κυρ Δεκ 21, 2008 9:03 pm
- Τοποθεσία: Ανθούπολη
Re: Ανάλυση,Θεωρητική - Όχι για μαθητές
Mπάμπη αυτήν την άσκηση την ξέρω με διάστημα,δηλαδή αν η f γνησίως μονότονη σε διάστημα [α,β]
αλλά και f([α,β])=[γ,δ] τότε να αποδείξετε ότι η f είναι συνεχής στο [α,β].
Εσύ δίνεις πάρα πολύ γήπεδο,το R,οπότε λέω να παίξω λίγη μπαλίτσα...
Xωρίς βλάβη της γενικότητας,υποθέτω πως f γνήσια αύξουσα στο R.
Έστω τυχαίο χ0 του R.Αφού το σύνολο τιμών είναι το R,θα υπάρχει ψ0 στο R,τέτοιο ώστε:
ψ1<ψ0<ψ2 όπου ψ1,ψ2 τυχαία σημεία του R και ψ0=f(x0).Έστω ε>0,αρκούντως μικρό τέτοιο ώστε:
ψ1<ψ0-ε<ψ0<ψ0+ε<ψ2.Απο την υπόθεση έχουμε πως υπάρχουν χ1,χ2 στο R ώστε f(x1)=ψ0-ε,f(x2)=ψ0+ε (1).
Τώρα για κάθε χ στο(χ1,χ2) έχουμε χ1<χ<χ2=> f(x1)<f(x)<f(x2) (2) απο τη μονοτονία της f .
Η σχέση (2) λόγω της (1) γίνεται: ψ0-ε<f(x)<ψ0+ε, ή καλύτερα
-ε<f(x)-ψ0<ε ή -ε<f(x)-f(x0)<ε ή |f(x)-f(x0)|<ε .Τούτο σημαίνει πως η f είναι συνεχής στο τυχαίο χ0 του R
αρα και σε όλο το R.
Με όμοιο τρόπο αν η f είναι γνησίως φθίνουσα στο R.
καλημέρα σε όλους!
αλλά και f([α,β])=[γ,δ] τότε να αποδείξετε ότι η f είναι συνεχής στο [α,β].
Εσύ δίνεις πάρα πολύ γήπεδο,το R,οπότε λέω να παίξω λίγη μπαλίτσα...
Xωρίς βλάβη της γενικότητας,υποθέτω πως f γνήσια αύξουσα στο R.
Έστω τυχαίο χ0 του R.Αφού το σύνολο τιμών είναι το R,θα υπάρχει ψ0 στο R,τέτοιο ώστε:
ψ1<ψ0<ψ2 όπου ψ1,ψ2 τυχαία σημεία του R και ψ0=f(x0).Έστω ε>0,αρκούντως μικρό τέτοιο ώστε:
ψ1<ψ0-ε<ψ0<ψ0+ε<ψ2.Απο την υπόθεση έχουμε πως υπάρχουν χ1,χ2 στο R ώστε f(x1)=ψ0-ε,f(x2)=ψ0+ε (1).
Τώρα για κάθε χ στο(χ1,χ2) έχουμε χ1<χ<χ2=> f(x1)<f(x)<f(x2) (2) απο τη μονοτονία της f .
Η σχέση (2) λόγω της (1) γίνεται: ψ0-ε<f(x)<ψ0+ε, ή καλύτερα
-ε<f(x)-ψ0<ε ή -ε<f(x)-f(x0)<ε ή |f(x)-f(x0)|<ε .Τούτο σημαίνει πως η f είναι συνεχής στο τυχαίο χ0 του R
αρα και σε όλο το R.
Με όμοιο τρόπο αν η f είναι γνησίως φθίνουσα στο R.
καλημέρα σε όλους!
Χρήστος Κυριαζής
-
k-ser
- Δημοσιεύσεις: 870
- Εγγραφή: Σάβ Δεκ 20, 2008 10:22 am
- Τοποθεσία: Μουζάκι Καρδίτσας
- Επικοινωνία:
Re: Ανάλυση,Θεωρητική - Όχι για μαθητές
Μπάμπη,
είχαμε συζητήσει ξανά το θέμα στο pathfinder.
Στο συνημμένο αρχείο, μια απάντησή μου για συνάρτηση γνησίως μονότονη σε διάστημα με σύνολο τιμών διάστημα.
Αν θυμάμαι καλά, είχα παιδευτεί αρκετά για μια "σχολική απάντηση" μα....
Να συμπληρώσω κάτι, για να μην αδικήσω την πολύ καλή προσέγγιση του Χρήστου:
Χρήστο, πολύ καλή η απόδειξή σου. Έχω την εντύπωση ότι τα ψ1, ψ2 δεν σου χρειάζονται!
είχαμε συζητήσει ξανά το θέμα στο pathfinder.
Στο συνημμένο αρχείο, μια απάντησή μου για συνάρτηση γνησίως μονότονη σε διάστημα με σύνολο τιμών διάστημα.
Αν θυμάμαι καλά, είχα παιδευτεί αρκετά για μια "σχολική απάντηση" μα....
Να συμπληρώσω κάτι, για να μην αδικήσω την πολύ καλή προσέγγιση του Χρήστου:
Χρήστο, πολύ καλή η απόδειξή σου. Έχω την εντύπωση ότι τα ψ1, ψ2 δεν σου χρειάζονται!
Κώστας Σερίφης
Re: Ανάλυση,Θεωρητική - Όχι για μαθητές
Δεν έχω δει τις παραπάνω λύσεις οπότε συγχωρέστε με αν είναι ίδια .
Σιλουανός Μπραζιτίκος
- chris_gatos
- Επιμελητής
- Δημοσιεύσεις: 6962
- Εγγραφή: Κυρ Δεκ 21, 2008 9:03 pm
- Τοποθεσία: Ανθούπολη
Re: Ανάλυση,Θεωρητική - Όχι για μαθητές
Kώστα μολις είδα το σχόλιο σου...Ναι έχεις δίκιο,αλλά τα έβαλα για να ''μαντρώσω'' πιο εύκολα,τις τιμές της f..
Διπλή προστασία!
Διπλή προστασία!
Χρήστος Κυριαζής
Re: Ανάλυση,Θεωρητική - Όχι για μαθητές
μιας και υποψιαζομαι οτι ο Κυριος Στεργιου εννοει την κουβεντα που ειχαμε σε αλλο φορουμ περι αυτης της προτασης να βαλω και εγω την λυση που ειχα βρει.
Χρησιμοποιω οπως ολοι τον επσιλοτικο ορισμο.
Αρκεί για κάθε να βρούμε
να βρούμε 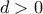 τέτοιο ώστε , για κάθε
τέτοιο ώστε , για κάθε  πραγματικο και
πραγματικο και  πραγματικο , να ισχυει:
πραγματικο , να ισχυει:
αν τότε
τότε 
έστω f γνησίως αύξουσα (για γν. φθινουσα λειτουργουμε ακριβως ομοια)
τότε ισχύει:


ορίζω σαν

ο ορισμός αυτός απαιτεί ,αφού οι τιμές ( ) τις οποίες παίρνει η αντίστροφη, διατρέχουν όλο το R (θυμίζω ότι το e διατρέχει όλο το (0,+infinite) )
) τις οποίες παίρνει η αντίστροφη, διατρέχουν όλο το R (θυμίζω ότι το e διατρέχει όλο το (0,+infinite) )
το σύνολο τιμών της να είναι το R ,συνθήκη που καλύπτεται από τα δεδομένα.
εύκολα βλέπουμε d>0
άρα από τον ορισμό του d έχουμε

και

επομένως παίρνουμε ότι
αν,

τότε

, που είναι ακρβώς το ζητούμενο.
Χρησιμοποιω οπως ολοι τον επσιλοτικο ορισμο.
Αρκεί για κάθε
 να βρούμε
να βρούμε 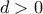 τέτοιο ώστε , για κάθε
τέτοιο ώστε , για κάθε  πραγματικο και
πραγματικο και  πραγματικο , να ισχυει:
πραγματικο , να ισχυει:αν
 τότε
τότε 
έστω f γνησίως αύξουσα (για γν. φθινουσα λειτουργουμε ακριβως ομοια)
τότε ισχύει:


ορίζω σαν

ο ορισμός αυτός απαιτεί ,αφού οι τιμές (
 ) τις οποίες παίρνει η αντίστροφη, διατρέχουν όλο το R (θυμίζω ότι το e διατρέχει όλο το (0,+infinite) )
) τις οποίες παίρνει η αντίστροφη, διατρέχουν όλο το R (θυμίζω ότι το e διατρέχει όλο το (0,+infinite) )το σύνολο τιμών της να είναι το R ,συνθήκη που καλύπτεται από τα δεδομένα.
εύκολα βλέπουμε d>0
άρα από τον ορισμό του d έχουμε

και

επομένως παίρνουμε ότι
αν,

τότε

, που είναι ακρβώς το ζητούμενο.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες
