 πίνακα
πίνακα  υπάρχει αντίστροφος να αποδειχθεί ότι είναι μοναδικός.
υπάρχει αντίστροφος να αποδειχθεί ότι είναι μοναδικός.β) Έστω ο πίνακας
![\left[ \begin{matrix}
1 & x & {{x}^{2}} \\
0 & 1 & 2x \\
0 & 0 & 1 \\
\end{matrix} \right] \left[ \begin{matrix}
1 & x & {{x}^{2}} \\
0 & 1 & 2x \\
0 & 0 & 1 \\
\end{matrix} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/19eff5ae4f7cf70ab925e565a7524fe2.png) τον οποίο συμβολίζουμε με
τον οποίο συμβολίζουμε με  . Να αποδειχθεί ότι :
. Να αποδειχθεί ότι :i)

ii)
 , (
, (  ο μοναδιαίος
ο μοναδιαίος  ).
).2. Δίνεται η συνάρτηση
 με
με  ,
,  η οποία μηδενίζεται στο
η οποία μηδενίζεται στο 
και παρουσιάζει τοπικό ακρότατο στο σημείο
 .
.α) Να βρεθούν τα

β) Να βρεθεί το είδος του ακροτάτου και η τιμή του.
3. α) Να αποδείξετε ότι :
''Αν οι συναρτήσεις
 με κοινό πεδίο ορισμού το διάστημα
με κοινό πεδίο ορισμού το διάστημα 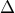 είναι παραγωγίσιμες στο
είναι παραγωγίσιμες στο 
τότε η συνάρτηση
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  και
και  ''.
''.β) Δίνεται η συνάρτηση
 με
με 
Να προσδιοριστεί το
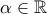 ώστε η συνάρτηση να είναι συνεχής στο
ώστε η συνάρτηση να είναι συνεχής στο  .
.4. Να αποδειχθεί ότι :
α) η συνάρτηση
 με
με  είναι γνησίως αύξουσα
είναι γνησίως αύξουσαβ) για
 :
:  και
και 

![\displaystyle{\begin{aligned}\left(f+g\right)^\prime(x_0)&=\lim_{x\to x_0}\frac{\left(f+g\right)(x)-\left(f+g\right)(x_0)}{x-x_0}\\&=\lim_{x\to x_0}\frac{f(x)+g(x)-f(x_0)-g(x_0)}{x-x_0}\\&=\lim_{x\to x_0}\left[\frac{f(x)-f(x_0)}{x-x_0}+\frac{g(x)-g(x_0)}{x-x_0}\right]\\&=f^\prime(x_0)+g^\prime(x_0)}\end{aligned}} \displaystyle{\begin{aligned}\left(f+g\right)^\prime(x_0)&=\lim_{x\to x_0}\frac{\left(f+g\right)(x)-\left(f+g\right)(x_0)}{x-x_0}\\&=\lim_{x\to x_0}\frac{f(x)+g(x)-f(x_0)-g(x_0)}{x-x_0}\\&=\lim_{x\to x_0}\left[\frac{f(x)-f(x_0)}{x-x_0}+\frac{g(x)-g(x_0)}{x-x_0}\right]\\&=f^\prime(x_0)+g^\prime(x_0)}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/ab12cfe57e33ccfbdc7c8eafadd8f88a.png)
 ως
ως , απαιτούμε
, απαιτούμε 




 τέτοια, ώστε
τέτοια, ώστε 




![\displaystyle{A\left( {{x_1}} \right) \cdot A\left( {{x_2}} \right) = \left[ {\begin{array}{*{20}{c}}
1&{{x_1}}&{x_1^2}\\
0&1&{2{x_1}}\\
0&0&1
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
1&{{x_2}}&{x_2^2}\\
0&1&{2{x_2}}\\
0&0&1
\end{array}} \right] = } \displaystyle{A\left( {{x_1}} \right) \cdot A\left( {{x_2}} \right) = \left[ {\begin{array}{*{20}{c}}
1&{{x_1}}&{x_1^2}\\
0&1&{2{x_1}}\\
0&0&1
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
1&{{x_2}}&{x_2^2}\\
0&1&{2{x_2}}\\
0&0&1
\end{array}} \right] = }](/forum/ext/geomar/texintegr/latexrender/pictures/1d0145c1a4c29eaf159d48890209ad02.png)
![\displaystyle{\left[ {\begin{array}{*{20}{c}}
1&{{x_1} + {x_2}}&{x_2^2 + 2{x_1}{x_2} + x_1^2}\\
0&1&{2{x_1} + 2{x_2}}\\
0&0&1
\end{array}} \right] = A\left( {{x_1} + {x_2}} \right)} \displaystyle{\left[ {\begin{array}{*{20}{c}}
1&{{x_1} + {x_2}}&{x_2^2 + 2{x_1}{x_2} + x_1^2}\\
0&1&{2{x_1} + 2{x_2}}\\
0&0&1
\end{array}} \right] = A\left( {{x_1} + {x_2}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/5b7eb805d15f75d1fbcaa8fb8776cc0b.png)
![\displaystyle{A\left( x \right) \cdot A\left( { - x} \right)\mathop = \limits^{\left( i \right)} A\left( {x - x} \right) = A\left( 0 \right) = \left[ {\begin{array}{*{20}{c}}
1&0&0\\
0&1&0\\
0&0&1
\end{array}} \right] = {I_3}} \displaystyle{A\left( x \right) \cdot A\left( { - x} \right)\mathop = \limits^{\left( i \right)} A\left( {x - x} \right) = A\left( 0 \right) = \left[ {\begin{array}{*{20}{c}}
1&0&0\\
0&1&0\\
0&0&1
\end{array}} \right] = {I_3}}](/forum/ext/geomar/texintegr/latexrender/pictures/cc4ba694ab7675d7d9f2e7bf55257c51.png)
 ως πολυωνυμική με παράγωγο
ως πολυωνυμική με παράγωγο  για κάθε
για κάθε 

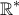 και παρουσιάζει τοπικό ακρότατο στο σημείο
και παρουσιάζει τοπικό ακρότατο στο σημείο 



 για κάθε
για κάθε 
 είναι ομόσημη του
είναι ομόσημη του  διότι
διότι  σε καθένα από τα διαστήματα
σε καθένα από τα διαστήματα 
 αφού
αφού 


 ορίζονται στο
ορίζονται στο 



 στο
στο 
 στο
στο  και στο
και στο ![\displaystyle{(0,2]} \displaystyle{(0,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/b1f3f4aedc7960c44c9310c6b378f150.png)
 στο
στο 
