 του επιπέδου ικανοποιούν τη σχέση
του επιπέδου ικανοποιούν τη σχέση  .
.i) Να αποδείξετε ότι

ii) Αν
 να εκφράσετε το διάνυσμα
να εκφράσετε το διάνυσμα  ως συνάρτηση των
ως συνάρτηση των 
β) Για τον αντιστρέψιμο πίνακα
 τύπου
τύπου  ορίζουμε τα πολυώνυμα
ορίζουμε τα πολυώνυμα 
όπου
 ο μοναδιαίος πίνακας
ο μοναδιαίος πίνακας  και
και  πραγματικός αριθμός.
πραγματικός αριθμός. Να αποδείξετε ότι αν
 τότε
τότε i)

ii)

2. α) Δίνεται η συνάρτηση
 και
και 
i) Να αποδείξετε ότι

ii) Να βρείτε το είδος της καμπύλης στην οποία ανήκουν τα σημεία
 για τα οποία οι μιγαδικοί αριθμοί
για τα οποία οι μιγαδικοί αριθμοί  με
με  ικανοποιούν την σχέση
ικανοποιούν την σχέση ![\displaystyle{Re}\left[ f(z) \right]=0} \displaystyle{Re}\left[ f(z) \right]=0}](/forum/ext/geomar/texintegr/latexrender/pictures/ad34f2d17d8f6466cf9f4e18ad129099.png)
β) Δίνεται η έλλειψη
 με
με  και το σημείο
και το σημείο  .
. Μια μεταβλητή ευθεία με συντελεστή διεύθυνσης
 διέρχεται από το σταθερό σημείο
διέρχεται από το σταθερό σημείο  και τέμνει τις εφαπτόμενες της έλλειψης
και τέμνει τις εφαπτόμενες της έλλειψης στα άκρα του μεγάλου άξονά της στα σημεία
 και
και  .
.i) Να βρείτε την εξίσωση του κύκλου με διάμετρο
 ως συνάρτηση του
ως συνάρτηση του  .
.ii) Να βρείτε την τιμή του
 ώστε ο κύκλος με διάμετρο
ώστε ο κύκλος με διάμετρο  να διέρχεται από τις εστίες της έλλειψης.
να διέρχεται από τις εστίες της έλλειψης.3. α) Να αποδείξετε ότι αν μια συνάρτηση
 είναι συνεχής στο
είναι συνεχής στο ![\displaystyle{\left[ \alpha ,\beta \right]} \displaystyle{\left[ \alpha ,\beta \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/c29ec413a22374a6bea5546f6066ad15.png) τότε
τότε i) Υπάρχουν
 τέτοια ώστε
τέτοια ώστε  .
.ii) Υπάρχει ένα τουλάχιστον
![\xi \in \left[ \alpha ,\beta \right] \xi \in \left[ \alpha ,\beta \right]](/forum/ext/geomar/texintegr/latexrender/pictures/541956efdba6b56f429c70b4dded784e.png) τέτοιο ώστε
τέτοιο ώστε 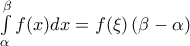 .
.β) Δίνεται η συνάρτηση
 με
με 
i) Να εξετάσετε την μονοτονία της συνάρτησης

ii) Να υπολογίσετε το

4. α) Δίνεται η ορθή γωνία
 και το ευθύγραμμο τμήμα
και το ευθύγραμμο τμήμα  μήκους
μήκους  m του οποίου τα άκρα
m του οποίου τα άκρα  και
και  ολισθαίνουν πάνω
ολισθαίνουν πάνω στις πλευρές
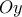 και
και  αντιστοίχως .
αντιστοίχως . Το σημείο
 κινείται με σταθερή ταχύτητα
κινείται με σταθερή ταχύτητα  m/sec και η θέση του πάνω στον άξονα
m/sec και η θέση του πάνω στον άξονα  δίνεται από τη συνάρτηση
δίνεται από τη συνάρτηση ![\displaystyle{s(t)=vt \,, t\in [0,5]} \displaystyle{s(t)=vt \,, t\in [0,5]}](/forum/ext/geomar/texintegr/latexrender/pictures/76b24b17b8828bedf4000399fc033f6f.png) όπου
όπου  ο χρόνος σε sec
ο χρόνος σε sec i) Να βρεθεί το εμβαδόν
 του τριγώνου
του τριγώνου  ως συνάρτηση του χρόνου.
ως συνάρτηση του χρόνου.ii) Ποιος είναι ο ρυθμός μεταβολής του εμβαδού
 τη στιγμή κατά την οποία το μήκος του τμήματος
τη στιγμή κατά την οποία το μήκος του τμήματος  είναι
είναι  m;
m;β) Να βρεθεί η συνεχής συνάρτηση
 για την οποία ισχύει
για την οποία ισχύει 


 πολλαπλάσιάζοντάς την με διάνυσμα
πολλαπλάσιάζοντάς την με διάνυσμα  θα γίνει:
θα γίνει:

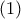 έχω:
έχω:  και αντικαθιστώ το γινόμενο
και αντικαθιστώ το γινόμενο 

 .
. και θέλουμε να δείξουμε ότι
και θέλουμε να δείξουμε ότι 
 τότε αφού
τότε αφού  ΑΤΟΠΟ, αφού ο πίνακας
ΑΤΟΠΟ, αφού ο πίνακας 




 και
και  ,
,  έχουμε,
έχουμε,



 και από το Πυθαγόρειο :
και από το Πυθαγόρειο :  επομένως για το εμβαδόν θα ισχύει :
επομένως για το εμβαδόν θα ισχύει : .
.
 . Έστω
. Έστω  η στιγμή που
η στιγμή που  .
. άρα ο
άρα ο 

 και άρα η
και άρα η  .
.
 και αφού η
και αφού η  .
. έχουμε :
έχουμε :  και από τη δοσμένη :
και από τη δοσμένη : 

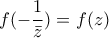
![\displaystyle{f(-\frac{1}{\bar{z}})=\frac{(-\frac{1}{\bar{z}}-1).[\frac{-1}{\bar{z}}+1]}{-\frac{1}{\bar{z}}+(-\frac{1}{\bar{\bar{z}}})}=} \displaystyle{f(-\frac{1}{\bar{z}})=\frac{(-\frac{1}{\bar{z}}-1).[\frac{-1}{\bar{z}}+1]}{-\frac{1}{\bar{z}}+(-\frac{1}{\bar{\bar{z}}})}=}](/forum/ext/geomar/texintegr/latexrender/pictures/5b6c423d2ab45824953abfdb791b35d3.png)




![\displaystyle{f(z)=\frac{(z-1).(\bar{z}+1)}{z+\bar{z}}=\frac{[(\alpha x-1)+\beta yi].[(\alpha x+1)-\beta yi]}{2\alpha x}=\frac{\alpha ^{2}.x^{2}-1-\alpha \beta xyi+\beta yi+\alpha \beta xyi+\beta yi+\beta ^{2}.y^{2}}{2\alpha x}=} \displaystyle{f(z)=\frac{(z-1).(\bar{z}+1)}{z+\bar{z}}=\frac{[(\alpha x-1)+\beta yi].[(\alpha x+1)-\beta yi]}{2\alpha x}=\frac{\alpha ^{2}.x^{2}-1-\alpha \beta xyi+\beta yi+\alpha \beta xyi+\beta yi+\beta ^{2}.y^{2}}{2\alpha x}=}](/forum/ext/geomar/texintegr/latexrender/pictures/74949f179ffd7d6c86edbc945e5be057.png)

![\displaystyle{Re[f(z)]=0\Leftrightarrow \frac{\alpha ^{2}\beta ^{2}+\beta ^{2}y^{2}-1}{2\alpha x}=0\overset{2\alpha x\neq 0}{\rightarrow} \alpha ^{2}\beta ^{2}+\beta ^{2}y^{2}-1=0} \displaystyle{Re[f(z)]=0\Leftrightarrow \frac{\alpha ^{2}\beta ^{2}+\beta ^{2}y^{2}-1}{2\alpha x}=0\overset{2\alpha x\neq 0}{\rightarrow} \alpha ^{2}\beta ^{2}+\beta ^{2}y^{2}-1=0}](/forum/ext/geomar/texintegr/latexrender/pictures/c81fbb01886fe618732ceaeb868f04f3.png)

 που σημαίνει ότι έχει τις εστίες τις στον άξονα
που σημαίνει ότι έχει τις εστίες τις στον άξονα 
 έχει εξίσωση
έχει εξίσωση 
 τα οποία είναι σημεία τομής της παραπάνω ευθείας με τις εφαπτομένες τις έλλειψης του μεγάλου άξονα προκύπτουν από τη λύση των δύο
τα οποία είναι σημεία τομής της παραπάνω ευθείας με τις εφαπτομένες τις έλλειψης του μεγάλου άξονα προκύπτουν από τη λύση των δύο


 αφού
αφού  .
.
 με
με 

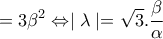
 ή
ή 
 είναι
είναι  στην οποία καταλήγουμε, παριστάνει έλλειψη.
στην οποία καταλήγουμε, παριστάνει έλλειψη.