 (σε μοίρες) αν γνωρίζουμε την εκκεντρότητα της τροχιάς
(σε μοίρες) αν γνωρίζουμε την εκκεντρότητα της τροχιάς  και τη μέση απόκλιση της τροχιάς
και τη μέση απόκλιση της τροχιάς  (μέση ανωμαλία).
(μέση ανωμαλία). Έχει τύπο
 (
(![M\epsilon [-\pi ,\pi ] M\epsilon [-\pi ,\pi ]](/forum/ext/geomar/texintegr/latexrender/pictures/65e183ac79cbd91d01b21f864dd0d3ad.png) και
και  ).
).Η άσκηση
Να αποδείξετε ότι η εξίσωση
 ,
,  έχει μοναδική ρίζα στο διάστημα
έχει μοναδική ρίζα στο διάστημα  .
.Συντονιστής: Καρδαμίτσης Σπύρος
 (σε μοίρες) αν γνωρίζουμε την εκκεντρότητα της τροχιάς
(σε μοίρες) αν γνωρίζουμε την εκκεντρότητα της τροχιάς  και τη μέση απόκλιση της τροχιάς
και τη μέση απόκλιση της τροχιάς  (μέση ανωμαλία).
(μέση ανωμαλία).  (
(![M\epsilon [-\pi ,\pi ] M\epsilon [-\pi ,\pi ]](/forum/ext/geomar/texintegr/latexrender/pictures/65e183ac79cbd91d01b21f864dd0d3ad.png) και
και  ).
). ,
,  έχει μοναδική ρίζα στο διάστημα
έχει μοναδική ρίζα στο διάστημα  .
.Ύπαρξηthanasis kopadis έγραψε:Να αποδείξετε ότι η εξίσωση,
έχει μοναδική ρίζα στο διάστημα
.
![\displaystyle{f(x)=x-e\sin x-1,~x\in[-1,2]} \displaystyle{f(x)=x-e\sin x-1,~x\in[-1,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/d2b45c734aa01688390e30e3f42ec170.png) η οποία είναι συνεχής ως άθροισμα συνεχών.
η οποία είναι συνεχής ως άθροισμα συνεχών.
 και
και  άρα
άρα 

 και
και  άρα
άρα 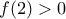 .
. από το θ. Bolzano, η συνάρτηση έχει μία τουλάχιστον ρίζα στο
από το θ. Bolzano, η συνάρτηση έχει μία τουλάχιστον ρίζα στο  .
. είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  . Η παράγωγος στο διάστημα
. Η παράγωγος στο διάστημα  μηδενίζεται μόνο για
μηδενίζεται μόνο για 
 άρα η ρίζα είναι μοναδική.
άρα η ρίζα είναι μοναδική.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες