1)
Έστω
 δύο συνεχείς συναρτήσεις τέτοιες ώστε για κάθε
δύο συνεχείς συναρτήσεις τέτοιες ώστε για κάθε  να ισχύει:
να ισχύει: και
και  . Αν η
. Αν η  τέμνει τον άξονα
τέμνει τον άξονα  σε δύο σημεία
σε δύο σημεία  εκατέρωθεν της αρχής των αξόνων, να δείξετε ότι η
εκατέρωθεν της αρχής των αξόνων, να δείξετε ότι η  τέμνει τον
τέμνει τον  σε ένα τουλάχιστον σημείο μεταξύ των
σε ένα τουλάχιστον σημείο μεταξύ των  και
και 
2)
Έστω
![f:[a,b]\rightarrow \mathbb R f:[a,b]\rightarrow \mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/3c0b0b46cd56a1e77fb9c66651948d2d.png) συνεχής συνάρτηση. Να αποδείξετε ότι για κάθε ζεύγος διαφορετικών σημείων
συνεχής συνάρτηση. Να αποδείξετε ότι για κάθε ζεύγος διαφορετικών σημείων  της
της  υπάρχει σημείο
υπάρχει σημείο  της
της  τέτοιο ώστε
τέτοιο ώστε 
3)
Δίνεται συνάρτηση
 συνεχής στο διάστημα
συνεχής στο διάστημα ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) . Έστω ότι τα σημεία
. Έστω ότι τα σημεία 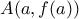 και
και  της
της  ορίζουν ευθεία
ορίζουν ευθεία  που είναι παράλληλη στον άξονα
που είναι παράλληλη στον άξονα  και ότι η
και ότι η  δεν έχει άλλο κοινό σημείο με τη
δεν έχει άλλο κοινό σημείο με τη  .
.Να αποδείξετε ότι υπάρχουν δύο τουλάχιστον σημεία
 της
της  με
με  παράλληλο στον άξονα
παράλληλο στον άξονα  τέτοια ώστε
τέτοια ώστε 
4)
Δίνεται συνάρτηση
 συνεχής στο διάστημα
συνεχής στο διάστημα ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) με
με  και
και 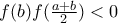 . Να αποδείξετε ότι υπάρχουν δύο τουλάχιστον σημεία
. Να αποδείξετε ότι υπάρχουν δύο τουλάχιστον σημεία  στο
στο  με απόσταση των τετμημενων
με απόσταση των τετμημενων  ίση με
ίση με  τέτοια ώστε
τέτοια ώστε 
5)
Δίνεται συνάρτηση
 συνεχής στο διάστημα
συνεχής στο διάστημα ![[0,4] [0,4]](/forum/ext/geomar/texintegr/latexrender/pictures/b839c0a45fd15dac69be08a4dbb0b7e3.png) , της οποίας η γραφική παράσταση βρίσκεται στο ορθογώνιο
, της οποίας η γραφική παράσταση βρίσκεται στο ορθογώνιο 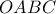 , όπου
, όπου  η αρχή των αξόνων και
η αρχή των αξόνων και  . Να δείξετε ότι η
. Να δείξετε ότι η  έχει ένα τουλάχιστον κοινό σημείο με καθεμία από τις διαγώνιες
έχει ένα τουλάχιστον κοινό σημείο με καθεμία από τις διαγώνιες 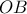 και
και  του ορθογωνίου.
του ορθογωνίου.
 δύο συνεχείς συναρτήσεις τέτοιες ώστε για κάθε
δύο συνεχείς συναρτήσεις τέτοιες ώστε για κάθε  να ισχύει:
να ισχύει: και
και  τα δύο σημεία, ισχύει ότι
τα δύο σημεία, ισχύει ότι  .
. , οπότε
, οπότε 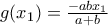 και
και 
 ετερόσημα, και τα
ετερόσημα, και τα  ετερόσημα, δηλαδή
ετερόσημα, δηλαδή 
 συνεχής, οπότε από θ.Bolzano υπάρχει ένα τουλάχιστον
συνεχής, οπότε από θ.Bolzano υπάρχει ένα τουλάχιστον  , τέτοιο ώστε
, τέτοιο ώστε 
 δύο σημεία της
δύο σημεία της με
με 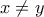
 είναι,
είναι,
![\displaystyle{c\in\left[a,b\right]-\left\{x,y\right\}} \displaystyle{c\in\left[a,b\right]-\left\{x,y\right\}}](/forum/ext/geomar/texintegr/latexrender/pictures/cad6f3d371f34da64f5abb536a460140.png) τέτοιο,
τέτοιο,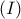
 , όπου
, όπου 
![\displaystyle{J_{x}=\left[x,y\right]\subset \left[a,b\right]} \displaystyle{J_{x}=\left[x,y\right]\subset \left[a,b\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/3ac6472a31453c6189533001760124fd.png) αν
αν 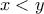 και
και ![\displaystyle{J_{y}=\left[x,y\right]\subset \left[a,b\right]} \displaystyle{J_{y}=\left[x,y\right]\subset \left[a,b\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/70949fa302372190ede79461b1214f4c.png) αν
αν 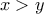 ,
,
 είναι συνεχής στο
είναι συνεχής στο  ως πράξεις συνεχών συναρτήσεων.
ως πράξεις συνεχών συναρτήσεων.
 .
. , υπάρχει
, υπάρχει ![\displaystyle{c\in J_{i}\subset \left[a,b\right]} \displaystyle{c\in J_{i}\subset \left[a,b\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/8fc8c4c6937c00b3977f59252c8891b8.png)
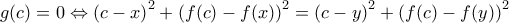 , όπως θέλαμε.
, όπως θέλαμε.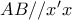 θα είναι
θα είναι  Η
Η  για κάθε
για κάθε  ή
ή  για κάθε
για κάθε 
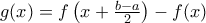 με
με ![x\in\left[a,\frac{a+b}{2}\right] . x\in\left[a,\frac{a+b}{2}\right] .](/forum/ext/geomar/texintegr/latexrender/pictures/becbc6c7a4490cdce1778db239afd6e3.png)
![\left[a,\frac{a+b}{2}\right] \left[a,\frac{a+b}{2}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/696a7b818d3759c5df555aa2cd684860.png) και
και 


 τέτοιος ώστε:
τέτοιος ώστε: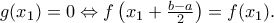
 και
και  όπου
όπου 
 και
και 
![g(a)\cdot g\left(\frac{a+b}{2}\right)=-\left[f\left(\frac{a+b}{2}\right)-f(a)\right]^2\leq 0 . g(a)\cdot g\left(\frac{a+b}{2}\right)=-\left[f\left(\frac{a+b}{2}\right)-f(a)\right]^2\leq 0 .](/forum/ext/geomar/texintegr/latexrender/pictures/81f157f2f34348ef7d0e1eff827433f8.png)
![x_1\in\left[a,\frac{a+b}{2}\right] . x_1\in\left[a,\frac{a+b}{2}\right] .](/forum/ext/geomar/texintegr/latexrender/pictures/8b5289a514ec7fa870a26f4e0e303291.png)
 και
και  ,
, 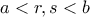 . Χωρίς βλάβη της γενικότητας, ας είναι
. Χωρίς βλάβη της γενικότητας, ας είναι  .
. , αυτό είναι προφανές, από το Θεώρημα ενδιάμεσων τιμών: το
, αυτό είναι προφανές, από το Θεώρημα ενδιάμεσων τιμών: το  .
. , θεωρούμε το ρόμβο
, θεωρούμε το ρόμβο  , δηλαδή με μια διαγώνιο να είναι το
, δηλαδή με μια διαγώνιο να είναι το  έχει τετμημένη
έχει τετμημένη  και το
και το  έχει τετμημένη
έχει τετμημένη  .
.![g:[r,s]\to \mathbb{R} g:[r,s]\to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/ba4afe6a09b03c95dd2c054010dc986d.png) η συνεχής (γραμμική) συνάρτηση που έχει ως γραφική παράσταση
η συνεχής (γραμμική) συνάρτηση που έχει ως γραφική παράσταση  . (To τμήμα
. (To τμήμα ![h:[r,s]\to \mathbb{R} h:[r,s]\to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/0e48c16077eda16627af9e650305d480.png) με
με  και παρατηρούμε ότι
και παρατηρούμε ότι  , οπότε το συμπέρασμα έπεται από το θεώρημα Bolzano.
, οπότε το συμπέρασμα έπεται από το θεώρημα Bolzano. , δηλαδή
, δηλαδή 
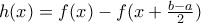 στο
στο ![[a,\frac{a+b}{2}] [a,\frac{a+b}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/e2e4c434ef37e8fee7e9a3a7dd218a5c.png)
 είναι συνεχής ως διαφορά συνεχών, με
είναι συνεχής ως διαφορά συνεχών, με  και
και  .
. , λόγω υπόθεσης. Άρα από Θ. Bolzano θα υπάρχει
, λόγω υπόθεσης. Άρα από Θ. Bolzano θα υπάρχει ![x_1\epsilon [a,\frac{a+b}{2}]\subseteq [a,b] x_1\epsilon [a,\frac{a+b}{2}]\subseteq [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3b10c813115e106f5f626c663889e7.png) τέτοιο ώστε
τέτοιο ώστε  και άρα αυτό που θέλαμε.
και άρα αυτό που θέλαμε. . Η διαγώνιος
. Η διαγώνιος  και άρα εξίσωση
και άρα εξίσωση  , ενώ αντίστοιχα η διαγώνιος
, ενώ αντίστοιχα η διαγώνιος 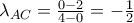 και εξίσωση
και εξίσωση 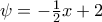 . Θεωρώ τις συναρτήσεις
. Θεωρώ τις συναρτήσεις  και
και  και εφαρμόζω το Θ.Bolzano για κάθεμια από αυτές στο διάστημα
και εφαρμόζω το Θ.Bolzano για κάθεμια από αυτές στο διάστημα ![f([0,4])=[0,2] f([0,4])=[0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/b6711b9aa42b12e90d6e4d51eefd4730.png) (λόγω του ορθογωνίου), οπότε
(λόγω του ορθογωνίου), οπότε 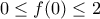 και
και  .
.