 τέτοιο ώστε η διχοτόμος
τέτοιο ώστε η διχοτόμος  της ορθής γωνίας
της ορθής γωνίας  , να ισούται με την πλευρά
, να ισούται με την πλευρά  . Να δειχτεί οτι
. Να δειχτεί οτι  .
.2. Δίνεται ισοσκελές τρίγωνο
 (
( ) και σημείο
) και σημείο 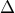 πάνω στην πλευρά του
πάνω στην πλευρά του  . Να αχθεί από το
. Να αχθεί από το  ευθεία, που να τέμνει την ευθεία
ευθεία, που να τέμνει την ευθεία  σε σημείο
σε σημείο  τέτοιο ώστε τα τρίγωνα
τέτοιο ώστε τα τρίγωνα  και
και 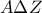 να είναι ισοδύναμα.
να είναι ισοδύναμα.3. Πάνω στην υποτείνουσα ορθογωνίου τριγώνου
 , φέρνουμε κάθετη σε τυχαίο σημείο
, φέρνουμε κάθετη σε τυχαίο σημείο  αυτής. Αυτή τέμνει την
αυτής. Αυτή τέμνει την  στο
στο 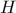 και την
και την  στο
στο  . Φέρνουμε την
. Φέρνουμε την  , η οποία τέμνει την
, η οποία τέμνει την  στο
στο  . Να βρεθεί ο γεωμετρικός τόπος του
. Να βρεθεί ο γεωμετρικός τόπος του  .
.4. α) Τα συμμετρικά σημεία
 του κέντρου
του κέντρου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  ως προς τις πλευρές
ως προς τις πλευρές  του τριγώνου αντίστοιχα , είναι κορυφές τριγώνου ίσου με το
του τριγώνου αντίστοιχα , είναι κορυφές τριγώνου ίσου με το  .
.β) Το ορθόκεντρο του σχηματισμένου αυτού τριγώνου, είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
 .
.γ) Οι ευθείες που συνδέουν τις κορυφές των ίσων γωνιών των δύο αυτών τριγώνων, διέρχονται από το μέσο του ευθύγραμμου τμήματος που συνδέει το
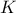 και το ορθόκεντρο του τριγώνου
και το ορθόκεντρο του τριγώνου  .
.5. Το επίπεδο που διέρχεται από τα μέσα δυο απέναντι ακμών τετραέδρου
 το διαιρεί σε δυο μέρη ισοδύναμα.
το διαιρεί σε δυο μέρη ισοδύναμα.
 που τέμνει την ευθεία
που τέμνει την ευθεία  στο
στο  . Προφανώς
. Προφανώς  . Προεκτείνουμε και την
. Προεκτείνουμε και την  προς το
προς το  κατά τμήμα
κατά τμήμα  .
. είναι συμμετρικά ως προς την μεσοκάθετο του
είναι συμμετρικά ως προς την μεσοκάθετο του  άρα είναι ίσα και έτσι
άρα είναι ίσα και έτσι  με άμεση συνέπεια και
με άμεση συνέπεια και  . Τότε όμως το τετράπλευρο
. Τότε όμως το τετράπλευρο  είναι εγγράψιμμο και άρα
είναι εγγράψιμμο και άρα  δηλαδή το τρίγωνο
δηλαδή το τρίγωνο  ισοσκελές και ορθογώνιο και θα είναι :
ισοσκελές και ορθογώνιο και θα είναι :  . Αλλά τα ορθογώνια τρίγωνα
. Αλλά τα ορθογώνια τρίγωνα 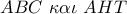 έχουν τις κάθετες πλευρές τους ίσες άρα θα είναι ίσα , οπότε θα έχουν
έχουν τις κάθετες πλευρές τους ίσες άρα θα είναι ίσα , οπότε θα έχουν  και άρα ή
και άρα ή  γίνεται :
γίνεται :  .
. ( εσωτερικό σημείο της
( εσωτερικό σημείο της  ) , είναι το ορθόκεντρο του
) , είναι το ορθόκεντρο του  , συνεπώς
, συνεπώς  , δηλαδή το
, δηλαδή το  ,
, 
 με
με 



 . Η κατασκευή δίνεται χωρίς άλλα λόγια ...
. Η κατασκευή δίνεται χωρίς άλλα λόγια ... ,
,  ,
,  τέμνουν τις πλευρές
τέμνουν τις πλευρές  ,
,  ,
,  του τριγώνου
του τριγώνου  , αντίστοιχα στα μέσα τους
, αντίστοιχα στα μέσα τους  ,
,  ,
,  .
. προκύπτει από το τρίγωνο
προκύπτει από το τρίγωνο  με την ομοιοθεσία κέντρου
με την ομοιοθεσία κέντρου  (κέντρο βάρους του
(κέντρο βάρους του  .
. προκύπτει από το
προκύπτει από το  και λόγου
και λόγου  .
. είναι ομοιόθετο του
είναι ομοιόθετο του  (Σύνθεση Ομοιοθεσιών).
(Σύνθεση Ομοιοθεσιών). εφόσον οι
εφόσον οι  ,
, 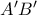 ,
, 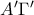 (τα ομοιόθετα τρίγωνα έχουν τις ομόλογες πλευρές τους παράλληλες).
(τα ομοιόθετα τρίγωνα έχουν τις ομόλογες πλευρές τους παράλληλες). ,
,  και
και  ,
,  και
και  ,
,  και
και  τα μέσα των πλευρών του τριγώνου
τα μέσα των πλευρών του τριγώνου  .
. είναι ρόμβοι( οι διαγώνιες διχοτομούνται και είναι κάθετες). Άρα τα τμήματα
είναι ρόμβοι( οι διαγώνιες διχοτομούνται και είναι κάθετες). Άρα τα τμήματα  είναι παράλληλα και ίσα, οπότε το τετράπλευρο
είναι παράλληλα και ίσα, οπότε το τετράπλευρο 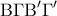 είναι παραλληλόγραμμο. Ομοίως και τα τετράπλευρα
είναι παραλληλόγραμμο. Ομοίως και τα τετράπλευρα 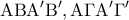 είναι παραλληλόγραμμα. Επομένως τα τρίγωνα
είναι παραλληλόγραμμα. Επομένως τα τρίγωνα  έχουν τις πλευρές τους παράλληλες και ίσες, οπότε είναι ίσα.
έχουν τις πλευρές τους παράλληλες και ίσες, οπότε είναι ίσα. , άρα
, άρα  είναι διαγώνιες των παραλληλογράμμων
είναι διαγώνιες των παραλληλογράμμων , οπότε διέρχονται από το ίδιο σημείο
, οπότε διέρχονται από το ίδιο σημείο  .
. , οπότε
, οπότε  και
και  .
. αντίστοιχα των ακμών
αντίστοιχα των ακμών  του τετραέδρου
του τετραέδρου  .
. αντίστοιχα στα σημεία
αντίστοιχα στα σημεία  .
.  βρίσκουμε την τομή
βρίσκουμε την τομή  αυτού με την
αυτού με την  .
. διέρχονται από το ίδιο σημείο, δηλαδή το
διέρχονται από το ίδιο σημείο, δηλαδή το  , έχουν ίδια βάση την
, έχουν ίδια βάση την  ισαπέχουν από το επίπεδο της βάσης καθώς το
ισαπέχουν από το επίπεδο της βάσης καθώς το 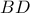 . Άρα:
. Άρα: 
 έχουν τον ίδιο όγκο.
έχουν τον ίδιο όγκο. 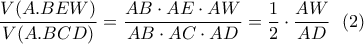


 με διατέμνουσα την
με διατέμνουσα την  . Άρα:
. Άρα: 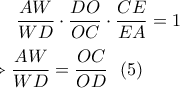
 με διατέμνουσα την
με διατέμνουσα την  . Άρα:
. Άρα: 

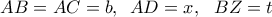 . Ο σκοπός μας είναι να υπολογίσουμε και να κατασκευάσουμε το τμήμα
. Ο σκοπός μας είναι να υπολογίσουμε και να κατασκευάσουμε το τμήμα  , με δεδομένα τα τμήματα
, με δεδομένα τα τμήματα  και με την προυπόθεση ότι
και με την προυπόθεση ότι  .
.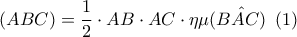 και ταυτόχρονα
και ταυτόχρονα 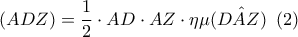
 . Έτσι το ευθύγραμμο τμήμα
. Έτσι το ευθύγραμμο τμήμα 
 .
. , ό.έ.δ.
, ό.έ.δ.
 (*)
(*)
 ,
, όπου
όπου  σημεία στον χώρο και ένα επίπεδο τέμνει την
σημεία στον χώρο και ένα επίπεδο τέμνει την  στο
στο  και την
και την  στο
στο 
