2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Γιώργος Απόκης · #21

GI_V_ALG_2_17736

Δίνεται η παράσταση : $\displaystyle{A=\frac{\eta\mu^2 x}{1-\sigma \upsilon \nu x}}$ με $\displaystyle{x\ne 2\kappa \pi,~\kappa\in\mathbb Z}$ .

α) Να αποδείξετε ότι $\displaystyle{A=1+\sigma\upsilon\nu x}$

β) Να λύσετε την εξίσωση $\displaystyle{\frac{\eta\mu^2 x}{1-\sigma \upsilon \nu x}=\frac{1}{2}}$ στο διάστημα $\displaystyle{(0,2\pi)}$

Λύση

α) $\displaystyle{A=\frac{\eta\mu^2 x}{1-\sigma \upsilon \nu x}=\frac{1-\sigma \upsilon \nu ^2 x}{1-\sigma \upsilon \nu x}=\frac{(1+\sigma \upsilon \nu x)(1-\sigma \upsilon \nu x)}{1-\sigma \upsilon \nu x}=1+\sigma \upsilon \nu x}$

β) Από το ερώτημα α), για $\displaystyle{x\ne 2\kappa \pi,~\kappa\in\mathbb Z}$ η εξίσωση είναι ισοδύναμη με την

$\displaystyle{1+\sigma \upsilon \nu x=\frac{1}{2}\Leftrightarrow \sigma \upsilon \nu x=-\frac{1}{2}=\sigma \upsilon \nu\frac{2\pi}{3}}$ και αφού $\displaystyle{x\in (0,2\pi) }$

έχουμε $\displaystyle{x=\frac{2\pi}{3}~\acute{\eta}~x=\frac{4\pi}{3}}$ (δεκτές)

#22

exdx έγραψε: GI_V_ALG_2_17650
(....)
Δίνεται ένα ορθογώνιο παραλληλόγραμμο με μήκος $\displaystyle{x\,\,cm}$ , πλάτος $\displaystyle{y\,\,cm}$ ,

Επομένως οι διαστάσεις του είναι $\displaystyle{x = 5,y = 14}$

Γιώργη καλησπέρα.

Δεν το είδα αναλυτικά, αλλά αναρωτιέμαι αν είναι σωστό να βγει το μήκος πιο μικρό από το πλάτος.

#23

GI_V_ALG_2_17664

Δίνονται οι γωνίες $\displaystyle \omega ,\;\theta$ για τις οποίες ισχύει: $\displaystyle \omega + \theta = 135^\circ$ .
Να αποδείξετε ότι:
α) $\displaystyle \varepsilon \phi \left( {\omega + \theta } \right) = - 1$ (Μονάδες 10)
β) $\displaystyle \varepsilon \phi \omega + \varepsilon \phi \theta + 1 = \varepsilon \phi \omega \cdot \varepsilon \phi \theta$ (Μονάδες 15)

ΛΥΣΗ:
α) Είναι $\displaystyle \varepsilon \phi \left( {\omega + \theta } \right) = \varepsilon \phi 135^\circ = \varepsilon \phi \left( {180^\circ - 45^\circ } \right) = - \varepsilon \phi 45^\circ = - 1$

β) Για τις τιμές των $\displaystyle \omega ,\;\theta$ , που ορίζονται οι $\displaystyle \varepsilon \phi \omega ,\;\varepsilon \phi \theta$ , δηλαδή για $\displaystyle \left\{ \begin{array}{l} \omega \ne \kappa \cdot 180^\circ + 90^\circ \\ \theta \ne \lambda \cdot 180^\circ + 90^\circ \\ \omega + \theta = 135^\circ \\ \end{array} \right.,\;\;\kappa ,\;\lambda \in {\rm Z}$
είναι
$\displaystyle \varepsilon \phi \left( {\omega + \theta } \right) = - 1 \Leftrightarrow \frac{{\varepsilon \phi \omega + \varepsilon \phi \theta }}{{1 - \varepsilon \phi \omega \cdot \varepsilon \phi \theta }} = - 1 \Leftrightarrow \varepsilon \phi \omega + \varepsilon \phi \theta + 1 = \varepsilon \phi \omega \cdot \varepsilon \phi \theta$

ΣΧΟΛΙΟ:
Νομίζω ότι οι περιορισμοί που γράψαμε παραπάνω θα έπρεπε ΟΠΩΣΔΗΠΟΤΕ είτε να ζητούνται (θα δυσκόλευε το θέμα) είτε να δίνονται στην εκφώνηση.

Επειδή παρατηρώ ότι στο φάκελο αυτό τις λύνουμε λιγάκι ανακατεμένες, μήπως θα μπορούσε κάποιος να γράψει ποιες απομένουν ;

#24

GI_V_ALG_2_17688

Δίνεται η συνάρτηση $\displaystyle f\left( x \right) = \frac{{2x}}{{x^2 + 1}}$

α) Να δείξετε ότι $\displaystyle f\left( x \right) \le 1$ . (Μονάδες 8)
β) Είναι το 1 η μέγιστη τιμή της συνάρτησης; Να αιτιολογήσετε την απάντησή σας.
(Μονάδες 8)
γ) Να εξετάσετε αν η συνάρτηση είναι άρτια ή περιττή. (Μονάδες 9)

ΛΥΣΗ:

α) Είναι $\displaystyle x^2 + 1 > 0$ , οπότε η $\displaystyle f\left( x \right)$ έχει Πεδίο Ορισμού όλο το $\displaystyle R$ .

Είναι $\displaystyle f\left( x \right) \le 1 \Leftrightarrow \frac{{2x}}{{x^2 + 1}} \le 1 \Leftrightarrow 2x \le x^2 + 1 \Leftrightarrow 0 \le x^2 - 2x + 1$

$\displaystyle \Leftrightarrow \left( {x - 1} \right)^2 \ge 0$ που ισχύει για κάθε $\displaystyle x \in R$ με το ίσον να ισχύει όταν $\displaystyle x = 1$

β) Όπως δείξαμε παραπάνω είναι $f(x) \le 1 \Leftrightarrow f(x) \le f(1)$ , οπότε η f(x)

έχει μέγιστο το

, όταν

.

γ) Η $\displaystyle f\left( x \right)$ έχει Π.Ο. όλο το

, οπότε για κάθε $\displaystyle x \in R$ θα είναι και $\displaystyle - x \in R$ με $\displaystyle f\left( { - x} \right) = \frac{{2\left( { - x} \right)}}{{\left( { - x} \right)^2 + 1}} = - \frac{{2x}}{{x^2 + 1}} = - f\left( x \right)$ , άρα η $\displaystyle f\left( x \right)$ είναι περιττή.

edit: Έκανα μια διόρθωση - συμπλήρωση με υπόδειξη του Κώστα Τηλέγραφου, τον οποίο ευχαριστώ.

pap65 · #25

Ετοιμάζω την 17692,17693
Να δηλώνει ο καθένας ποιά κάνει

pap65 · #26

ΘΕΜΑ 2-17692

α) Να αποδείξετε ότι: $\eta \mu \left( \frac{\pi }{2}+x \right)+\sigma \upsilon \nu \left( \pi +x \right)=0$ (Μονάδες 10)
β) Να βρείτε τις τιμές του $\displaystyle{x\in \left[ 0,2\pi \right)}$ για τις οποίες ισχύει: $\sigma \upsilon \nu x=-\eta \mu \left( \frac{\pi }{2}+x \right)$
(Μονάδες 15)

ΛΥΣΗ

Α) Ισχύει : $\eta \mu \left( \frac{\pi }{2}+x \right)=\eta \mu \left( \frac{\pi }{2}-x \right)$

( Αφού $\left( \frac{\pi }{2}+ \right)+\left( \frac{\pi }{2}- \right)=\pi$ )
Όμως $\eta \mu \left( \frac{\pi }{2}-x \right)=\sigma \upsilon \nu x$
( γωνίες συμπληρωματικές )
Δηλαδή $\eta \mu \left( \frac{\pi }{2}+x \right)=\sigma \upsilon \nu x$ .

Ακόμη $\sigma \upsilon \nu \left( \pi +x \right)=-\sigma \upsilon \nu x$
(γωνίες που διαφέρουν κατά π )

Συνεπώς $\eta \mu \left( \frac{\pi }{2}+x \right)+\sigma \upsilon \nu \left( \pi +x \right)=\sigma \upsilon \nu x-\sigma \upsilon \nu x=0$

Β) Είναι $\sigma \upsilon \nu x=-\eta \mu \left( \frac{\pi }{2}+x \right)\Leftrightarrow \sigma \upsilon \nu x=-\sigma \upsilon \nu x$ ( Από το α ερώτημα )
$\Leftrightarrow 2\sigma \upsilon \nu x=0\Leftrightarrow \sigma \upsilon \nu x=0$

$\Leftrightarrow \sigma \upsilon \nu x=\sigma \upsilon \nu \frac{\pi }{2}\Leftrightarrow x=2\kappa \pi \pm \frac{\pi }{2}$ , $\kappa \in \mathbb{Z}$ .

Όμως $\displaystyle{x\in \left[ 0,2\pi \right)}$ , επομένως

• $\displaystyle{0\le 2\kappa \pi +\frac{\pi }{2}<2\pi \overset{\cdot 2}{\mathop{\Leftrightarrow }}\,0\le 4\kappa +<4}$

$\displaystyle{\Leftrightarrow 0\le 4\kappa +1<4\Leftrightarrow -1\le 4\kappa <3\Leftrightarrow \frac{-1}{4}\le \kappa <\frac{3}{4}}$ , με $\kappa \in \mathbb{Z}$

Άρα $\kappa =0$ και $x=\frac{\pi }{2}$

• $\displaystyle{0\le 2\kappa \pi -\frac{\pi }{2}<2\pi \overset{\cdot 2}{\mathop{\Leftrightarrow }}\,0\le 4\kappa -<4}$

$\displaystyle{\Leftrightarrow 0\le 4\kappa -1<4\Leftrightarrow 1\le 4\kappa <5\Leftrightarrow \frac{1}{4}\le \kappa <\frac{5}{4}}$ , με $\kappa \in \mathbb{Z}$

Άρα $\kappa =1$ και $x=2\pi -\frac{\pi }{2}=\frac{3\pi }{2}$

ΕΓΙΝΕ ΔΙΟΡΘΩΣΗ ΣΤΗΝ ΠΡΩΤΗ ΛΥΣΗ ( $x=\frac{\pi }{2}$ ) ΥΣΤΕΡΑ ΑΠΟ Π. Μ. ΤΟΥ dimkat

#27

GI_V_ALG_2_17656

Δίνεται η συνάρτηση $\displaystyle{f(x) = \frac{1}{2}\sigma \upsilon \nu 2x,x \in R}$
α) Ποια είναι η μέγιστη και ποια η ελάχιστη τιμή της συνάρτησης; Ποια είναι η περίοδος της

;
(Μονάδες

)
β) Να σχεδιάσετε τη γραφική παράσταση της

σε διάστημα πλάτους μιας περιόδου.
(Μονάδες 10)
γ) Να εξετάσετε αν η συνάρτηση μπορεί να πάρει την τιμή

. Να αιτιολογήσετε την απάντησή
σας. (Μονάδες

)

Λύση.

α) Η

έχει ελάχιστη τιμή $\displaystyle{ - \frac{1}{2}}$ και μέγιστη τιμή $\displaystyle{ \frac{1}{2}}$ . Κάθε τιμή της συνάρτησης επαναλαμβάνεται όταν το

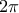αυξηθεί κατά $2\pi$ , οπότε το

αυξάνεται κατά $\pi$ . Επομένως η περίοδος της

είναι $T=\pi$ .

β)

: 2_17656.png (5.7 KiB) Προβλήθηκε 5545 φορές

γ) Η συνάρτηση δεν μπορεί να πάρει την τιμή

, επειδή έχει μέγιστη τιμή το $\displaystyle{ \frac{1}{2}}$ . Αυτό άλλωστε φαίνεται και πιο πάνω στη γραφική παράσταση. Η

δεν μπορεί να πάρει τιμές εκτός του διαστήματος $\displaystyle{\left[ { - \frac{1}{2},\frac{1}{2}} \right]}$ .

ΣΧΟΛΙΟ: Το β) ερώτημα είναι κάπως ασαφές. Το διάστημα πλάτους μιας περιόδου μπορεί να είναι οποιοδήποτε διάστημα έχει πλάτος $\pi$ , π. χ το $\displaystyle{\left[ {\frac{{3\pi }}{4},\frac{{7\pi }}{4}} \right]}$ .

#28

ΑΠΟ ΓΙΩΡΓΟ ΛΕΚΚΑ
ΘΕΜΑ 2 - 17717
ΛΥΣΗ
α) Είναι $\left.\begin{matrix} 16x+14y=374 & \\ x+y=25 & \end{matrix}\right\}$ .

β) $\left.\begin{matrix} 16x+14y=374 & \\ x+y=25 & \end{matrix}\right\}\Leftrightarrow \left.\begin{matrix} 16(25-y)+14y=374 & \\ x=25-y & \end{matrix}\right\}\Leftrightarrow \left.\begin{matrix} y=13 & \\ x=12 & \end{matrix}\right\}$ .

Παρατήρηση
Θα μπορούσε να ζητήσει τον αριθμό των καθισμάτων στο κάτω και στο πάνω διάζωμα.
Απάντηση
Κάτω διάζωμα: $16 \cdot 12=192$ καθίσματα.
Πάνω διάζωμα: $14 \cdot 13=182$ καθίσματα.

Ιστοσελίδα · #29

18632

Στο παρακάτω σχήμα δίνονται οι παραβολές C_f , C_g

που είναι γραφικές παραστάσεις των συναρτήσεων f, g

αντίστοιχα με πεδίο ορισμού το $\mathbb{R}$ . Η γραφική παράσταση της

προκύπτει από τη γραφική παράσταση της

με οριζόντια και κατακόρυφη μετατόπιση. Παρατηρώντας το σχήμα:
α) Να βρείτε τα διαστήματα μονοτονίας, το είδος του ακρότατου της

και την τιμή του. (Μονάδες 10)

β) Να βρείτε μέσω ποιων μετατοπίσεων της C_f

προκύπτει η C_g

. (Μονάδες 15)

: 18632.JPG (17.78 KiB) Προβλήθηκε 5548 φορές

Λύση

α) Η συνάρτηση

είναι γνησίως φθίνουσα στο διάστημα $(-\infty , -2]$ και γνησίως αύξουσα στο διάστημα $[-2, +\infty)$
Παρουσιάζει ελάχιστη τιμή για x=-2

την

.

β) Παρατηρούμε ότι η C_g

προκύπτει από την C_f

, αν αυτή μετατοπιστεί κατά 4 μονάδες δεξιά και 4 μονάδες κάτω.
Δηλαδή: g(x) = f(x-4) -4

για κάθε $x \in \mathbb{R}$ .

asemarak · #30

GI_V_ALG_2_17663

Αν $0<x<\frac{\pi }{2}$ και $(2 \sigma\upsilon \nu x+1)\cdot (5 \sigma\upsilon \nu x-4)=0$ , τότε:
α) Να αποδείξετε ότι $\sigma\upsilon \nu x=\frac{4}{5}$ . (Μονάδες 10)
β) Να βρείτε τους άλλους τριγωνομετρικούς αριθμούς της γωνίας x. (Μονάδες 15)

ΛΥΣΗ

α) Αφού $0<x<\frac{\pi }{2}$ (1ο τεταρτημόριο), είναι $\sigma\upsilon \nu x>0$ .

$(2 \sigma\upsilon \nu x+1)\cdot (5 \sigma\upsilon \nu x-4)=0$ $\Leftrightarrow 2 \sigma\upsilon \nu x+1=0$ ή $5 \sigma\upsilon \nu x-4=0$ $\Leftrightarrow \sigma\upsilon \nu x=-\frac{1}{2}$ ή $\sigma\upsilon \nu x=\frac{4}{5}$ .

Αφού $\sigma\upsilon \nu x>0$ , δεκτό είναι μόνο το $\sigma\upsilon \nu x=\frac{4}{5}$ .

β) Ισχύει ότι $\eta \mu ^{2}x+\sigma \upsilon \nu ^{2}x=1\Leftrightarrow \eta \mu ^{2}x + \left ( \frac{4}{5} \right )^{2}=1\Leftrightarrow \eta \mu ^{2}x + \left \frac{16}{25} \right =1 \Leftrightarrow \eta \mu ^{2}x =\frac{9}{25}$ .

Άρα $\eta \mu x=\frac{3}{5}$ ή $\eta \mu x=-\frac{3}{5}$ . Επειδή $\eta \mu x>0$ , για κάθε x με $0<x<\frac{\pi }{2}$ , είναι τελικά $\eta \mu x=\frac{3}{5}$ .

Επίσης $\varepsilon \phi x=\frac{\eta \mu x}{\sigma \upsilon \nu x}=\frac{\frac{3}{5}}{\frac{4}{5}}=\frac{3}{4}$ και $\sigma \phi x=\frac{1}{\varepsilon \phi x}=\frac{1}{\frac{3}{4}}=\frac{4}{3}$ .

#31

Νομίζω ότι απομένουν οι παρακάτω:

2_16954
2_17659
2_17681
2_17683
2_17698
2_17699
2_17703
2_17704
2_17709
2_17725

Ας το ελέγξει όμως και κάποιος άλλος.

#32

GI_V_ALG_2_17659

α) Να λύσετε αλγεβρικά το σύστημα $\displaystyle{\left\{ \begin{array}{l} y = {x^2} + 1\\ x - y = - 1 \end{array} \right.}$
(Μονάδες

)
β) Να ερμηνεύσετε γεωμετρικά τις λύσεις του συστήματος που βρήκατε στο ερώτημα α).
(Μονάδες

)

Λύση.

α) $\displaystyle{\left\{ \begin{array}{l} y = {x^2} + 1\\ x - y = - 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} y = {x^2} + 1\\ y = x + 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x + 1 = {x^2} + 1\\ y = x + 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x(x - 1) = 0\\ y = x + 1 \end{array} \right. \Leftrightarrow }$

(x=0,y=1)

ή

β) Οι λύσεις του συστήματος είναι τα σημεία τομής της παραβολής με εξίσωση y=x^2+1

και της ευθείας με εξίσωση y=x+1

, όπως φαίνεται παρακάτω.

: 2_17659.png (12.6 KiB) Προβλήθηκε 5507 φορές

Γιώργος Απόκης · #33

GI_V_ALG_2_17725

Δίνεται η συνάρτηση $\displaystyle{f(x)=\eta \mu (\pi-3x)+\sigma \upsilon \nu \left(\frac{\pi}{2}-3x\right)}$ .

α) Να δείξετε ότι $\displaystyle{f(x)=2\eta\mu 3x}$

β) Να σχεδιάσετε τη γραφική παράσταση της $\displaystyle{f}$ .

Λύση

α) Έχουμε $\displaystyle{\eta \mu (\pi-3x)=\eta \mu 3x}$ και $\displaystyle{\sigma \upsilon \nu \left(\frac{\pi}{2}-3x\right)=\eta \mu 3x}$ άρα

με αντικατάσταση προκύπτει $\displaystyle{f(x)=2\eta\mu 3x}$ .

β) Η συνάρτηση έχει μέγιστο $\displaystyle{2}$ , ελάχιστο $\displaystyle{-2}$ και περίοδο $\displaystyle{T=\frac{2\pi}{3}}$

asemarak · #34

GI_V_ALG_2_17699

Δίνεται $\eta \mu \phi =\frac{3}{5}$ , όπου φ η οξεία γωνία που σχηματίζεται με κορυφή το σημείο Α της ευθείας (ε) του παρακάτω σχήματος.
Εικόνα

α) Να βρείτε το συνημίτονο της γωνίας φ. (Μονάδες 10)
β) Να βρείτε το ημίτονο και το συνημίτονο των γωνιών θ και ω του σχήματος. (Μονάδες 15)

ΛΥΣΗ

α) Ισχύει $\eta \mu^{2} \phi +\sigma \upsilon \nu ^{2}\phi =1\Leftrightarrow \left ( \frac{3}{5} \right )^{2}+\sigma \upsilon \nu ^{2}\phi =1 \Leftrightarrow \frac{9}{25}+\sigma \upsilon \nu ^{2}\phi =1 \Leftrightarrow \sigma \upsilon \nu ^{2}\phi = \frac{16}{25}$

$\Leftrightarrow \sigma \upsilon \nu \phi =\frac{4}{5}$ ή $\sigma \upsilon \nu \phi =-\frac{4}{5}$ .

Αφού η γωνία φ είναι οξεία, είναι $\sigma \upsilon \nu \phi >0$ και επομένως $\sigma \upsilon \nu \phi =\frac{4}{5}$ .

β) Παρατηρούμε ότι η γωνία ω είναι παραπληρωματική της φ, οπότε $\omega =\pi -\phi$ .

Έτσι $\eta \mu \omega =\eta \mu(\pi -\phi )=\eta \mu \phi =\frac{3}{5}$ και $\sigma \upsilon \nu \omega =\sigma \upsilon \nu (\pi -\phi )=-\sigma \upsilon \nu \phi =-\frac{4}{5}$ .

Επίσης $\theta =2\pi -\omega$ , οπότε

$\eta \mu \theta = \eta \mu(2\pi -\omega )=\eta \mu( -\omega )=-\eta \mu \omega =-\frac{3}{5}$

και $\sigma \upsilon \nu \theta = \sigma \upsilon \nu (2\pi -\omega )=\sigma \upsilon \nu ( -\omega )=\sigma \upsilon \nu \omega =-\frac{4}{5}$ .

* Στα ίδια συμπεράσματα θα καταλήγαμε αν παρατηρούσαμε ότι $\theta =\pi +\phi$ (ίσως να λυνόταν στο πι και φι)

* Μήπως τα θέματα της Β΄ Λυκείου (Άλγεβρας και Γεωμετρίας) είναι ευκολότερα από τα αντίστοιχα της Α΄ Λυκείου ή εμένα μου φαίνεται;

Γιώργος Απόκης · #35

GI_V_ALG_2_17709

Δίνονται οι ευθείες $\displaystyle{\epsilon_1:2x+y=5,~~\epsilon_2:-2x+3y=-9,~~\epsilon_1:3x+2y=7}$

α) i) Να βρείτε τις συντεταγμένες του σημείου τομής των $\displaystyle{\epsilon_1,~\epsilon_2}$

ii) Να βρείτε τις συντεταγμένες του σημείου τομής των $\displaystyle{\epsilon_1,~\epsilon_3}$

β) Με τη βοήθεια του ερωτήματος α) να δείξετε ότι το κοινό σημείο των $\displaystyle{\epsilon_2,~\epsilon_3}$ είναι σημείο της $\displaystyle{\epsilon_1}$

Λύση

α) i) Λύνουμε το σύστημα $\displaystyle{\begin{cases} ~~~2x+y=5\\-2x+3y=-9 \end{cases}}$ . Προσθέτουμε κατά μέλη : $\displaystyle{4y=-4\Leftrightarrow y=-1}$

και με αντικατάσταση στη 1η : $\displaystyle{2x-1=5\Leftrightarrow x=3}$ άρα το σημείο τομής είναι το $\displaystyle{A(3,-1)}$ .

ii) Λύνουμε το σύστημα $\displaystyle{\begin{cases} 2x+y=5\\3x+2y=7 \end{cases}\Leftrightarrow\begin{cases}-4x-2y=-10\\3x+2y=7 \end{cases}}$ . Προσθέτουμε κατά μέλη : $\displaystyle{-x=-3\Leftrightarrow x=3}$

και με αντικατάσταση στη 1η : $\displaystyle{6+y=5\Leftrightarrow y=-1}$ άρα το σημείο τομής είναι το $\displaystyle{A(3,-1)}$ .

β) Παρατηρούμε ότι οι τρεις ευθείες έχουν κοινό σημείο το $\displaystyle{A(3,-1)}$ , άρα προφανώς το κοινό σημείο των $\displaystyle{\epsilon_2,~\epsilon_3}$

(που είναι μοναδικό αφού αυτές δεν είναι παράλληλες, ούτε συμπίπτουν) είναι σημείο της $\displaystyle{\epsilon_1}$

Edit : Tα μπλε. Ευχαριστώ τον dimkat για την επισήμανση

Γιώργος Απόκης · #36

GI_V_ALG_2_17683

Δίνεται το σύστημα : $\displaystyle{\begin{cases} (\lambda+1)x+2y=3\\4x+(\lambda-1)y=-6 \end{cases}}$ με παράμετρο $\displaystyle{\lambda \in \mathbb R}$ .

α) Αν $\displaystyle{\lambda=-3}$ , να δείξετε ότι το σύστημα έχει άπειρες λύσεις. Να βρείτε μία λύση.

β) Αν $\displaystyle{\lambda=3}$ , να δείξετε ότι το σύστημα είναι αδύνατο.

γ) Αν $\displaystyle{\lambda=0}$ , να δείξετε ότι το σύστημα έχει μοναδική λύση την οποία και να προσδιορίσετε.

Λύση

α) Για $\displaystyle{\lambda=-3 }$ έχουμε $\displaystyle{\begin{cases} -2x+2y=3\\4x-4y=-6 \end{cases}\Leftrightarrow y=x+\frac{3}{2},~x\in \mathbb R}$ (άπειρες λύσεις).

Για $\displaystyle{x=\frac{1}{2}}$ έχουμε $\displaystyle{y=2}$ άρα μια λύση είναι η $\displaystyle{(x,y)=\left(\frac{1}{2},2\right)}$ .

β) Για $\displaystyle{\lambda=3 }$ έχουμε $\displaystyle{\begin{cases} 4x+2y=3\\4x+2y=-6 \end{cases}$ (αδύνατο).

γ) Για $\displaystyle{\lambda=0 }$ έχουμε $\displaystyle{\begin{cases} x+2y=3\\4x-y=-6 \end{cases}\Leftrightarrow \begin{cases} x+2y=3\\8x-2y=-12 \end{cases}$ . Προσθέτουμε κατά μέλη:

$\displaystyle{9x=-9\Leftrightarrow x=-1}$ και με αντικατάσταση στην 1η : $\displaystyle{-1+2y=3\Leftrightarrow y=2}$

Γιώργος Απόκης · #37

GI_V_ALG_2_16954

Δίνεται η εξίσωση : $\displaystyle{8x+2y=7~(1)}$

α) Να γράψετε μια άλλη εξίσωση που να μην έχει καμία κοινή λύση με την (1)

β) Να παραστήσετε γραφικά τις δύο εξισώσεις και, με βάση το γράφημα, να εξηγήσετε γιατί το σύστημα είναι αδύνατο.

Λύση

α) Πρέπει το σύστημα να είναι αδύνατο, άρα επιλέγουμε π.χ. $\displaystyle{8x+2y=11}$

β) Παρατηρούμε ότι οι ευθείες είναι παράλληλες, άρα το σύστημα είναι αδύνατο

Γιώργος Απόκης · #38

Μένουν οι παρακάτω:

17681
17698
17703
17704

pap65 · #39

ΘΕΜΑ 2-17693

α) Να διατάξετε από το μικρότερο στο μεγαλύτερο τους παρακάτω αριθμούς:

$\sigma \upsilon \nu \frac{\pi }{6},\quad \sigma \upsilon \nu \frac{\pi }{4},\quad \sigma \upsilon \nu \frac{17\pi }{10}$ (Μονάδες 12)

β) Αν $\pi <{{x}_{1}}<{{x}_{2}}<\frac{3\pi }{2}$ , να συγκρίνετε τους αριθμούς:

$\displaystyle{\eta \mu \left( \frac{\pi }{2}-{{x}_{1}} \right),\quad \eta \mu \left( \frac{\pi }{2}-{{x}_{2}} \right)}$ (Μονάδες 13)

ΛΥΣΗ

Α) Κάνω αναγωγή στο πρώτο τεταρτημόριο για το $\sigma \upsilon \nu \frac{17\pi }{10}$

Χρησιμοποιώντας διαδοχικά γωνίες που διαφέρουν κατά $\pi$

Και στην συνέχεια γωνίες που έχουν άθροισμα $\pi$ παίρνουμε:

$\sigma \upsilon \nu \frac{17\pi }{10}=\sigma \upsilon \nu \left( \pi +\frac{7\pi }{10} \right)=-\sigma \upsilon \nu \frac{7\pi }{10}=\sigma \upsilon \nu \frac{3\pi }{10}$

( Αφού $\frac{7\pi }{10}+\frac{3\pi }{10}=\pi$ )

Έτσι οι γωνίες $\frac{\pi }{6},\quad \frac{\pi }{4},\quad \frac{3\pi }{10}$ ανήκουν στο διάστημα $\left[ 0,\frac{\pi }{2} \right]$

που όπως γνωρίζουμε η συνάρτηση του $\sigma \upsilon \nu$ είναι γνησίως φθίνουσα.

Επομένως: $\frac{\pi }{6}<\frac{\pi }{4}<\frac{3\pi }{10}\Rightarrow \sigma \upsilon \nu \frac{\pi }{6}>\sigma \upsilon \nu \frac{\pi }{4}>\sigma \upsilon \nu \frac{3\pi }{10}$

Β) Α ΤΡΟΠΟΣ

Ισχύει ότι $\displaystyle{\eta \mu \left( \frac{\pi }{2}-{{x}_{1}} \right)=\sigma \upsilon \nu {{x}_{1}}}$ ( Γωνίες συμπληρωματικές )

Και $\displaystyle{\eta \mu \left( \frac{\pi }{2}-{{x}_{2}} \right)=\sigma \upsilon \nu {{x}_{2}}}$ ( Γωνίες συμπληρωματικές )

Ισχύει ότι $\pi <{{x}_{1}}<{{x}_{2}}<\frac{3\pi }{2}$ δηλαδή ${{x}_{1}},{{x}_{2}}\in \left( \pi ,\frac{3\pi }{2} \right)$ .

Στο διάστημα αυτό η συνάρτηση του $\sigma \upsilon \nu$ είναι γνησίως αύξουσα.

Επομένως: ${{x}_{1}}<{{x}_{2}}\Rightarrow \sigma \upsilon \nu {{x}_{1}}<\sigma \upsilon \nu {{x}_{2}}\Leftrightarrow \eta \mu \left( \frac{\pi }{2}-{{x}_{1}} \right)<\eta \mu \left( \frac{\pi }{2}-{{x}_{2}} \right)$

Β ΤΡΟΠΟΣ

Αφού $\pi <{{x}_{1}}<{{x}_{2}}<\frac{3\pi }{2}\overset{\cdot \left( -1 \right)}{\mathop{\Leftrightarrow }}\,-\pi >-{{x}_{1}}>-{{x}_{2}}>-\frac{3\pi }{2}$

$\overset{+\frac{\pi }{2}}{\mathop{\Leftrightarrow }}\,\frac{\pi }{2}-\pi >\frac{\pi }{2}-{{x}_{1}}>\frac{\pi }{2}-{{x}_{2}}>\frac{\pi }{2}- \frac{3\pi }{2}$
$\Leftrightarrow -\frac{\pi }{2}>\frac{\pi }{2}-{{x}_{1}}>\frac{\pi }{2}-{{x}_{2}}>-\pi$

Άρα οι γωνίες $\displaystyle{\frac{\pi }{2}-{{x}_{1}},\quad \frac{\pi }{2}-{{x}_{2}}}$

ανήκουν στο διάστημα $\left( -\pi ,-\frac{\pi }{2} \right)$

που όπως γνωρίζουμε η συνάρτηση του $\eta \mu$ είναι γνησίως φθίνουσα.

Επομένως: $\frac{\pi }{2}-{{x}_{1}}>\frac{\pi }{2}-{{x}_{2}}\Leftrightarrow \eta \mu \left( \frac{\pi }{2}-{{x}_{1}} \right)<\eta \mu \left( \frac{\pi }{2}-{{x}_{2}} \right)$ .

Γιώργος Απόκης · #40

GI_V_ALG_2_17681

Δίνεται η συνάρτηση $\displaystyle{f(x)=2\eta\mu x+1,~x\in\mathbb R}$

α) Να βρείτε τη μέγιστη και την ελάχιστη τιμή της $\displaystyle{f}$

β) Για ποια τιμή του $\displaystyle{x\in[0,2\pi]}$ η συνάρτηση παρουσιάζει μέγιστη τιμή;

Λύση

α) H συνάρτηση $\displaystyle{g(x)=2\eta\mu x}$ έχει ελάχιστη τιμή $\displaystyle{-2}$ και μέγιστη $\displaystyle{2}$ , άρα η $\displaystyle{f(x)=g(x)+1}$

θα έχει ελάχιστη τιμή $\displaystyle{-2+1=-1}$ και μέγιστη $\displaystyle{2+1=3}$ .

β) Έχουμε $\displaystyle{f(x)=3\Leftrightarrow 2\eta\mu x+1=3\Leftrightarrow 2\eta\mu x=2\Leftrightarrow \eta\mu x=1=\eta\mu \frac{\pi}{2} }$

και αφού $\displaystyle{x\in[0,2\pi]}$ έχουμε $\displaystyle{x=\frac{\pi}{2}}$

2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ

Μέλη σε σύνδεση