Αρχιμήδης 2014-2015
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Αρχιμήδης 2014-2015
Θα παρακαλούσα τα έμπειρα μέλη του mathematica να βάλουν ασκήσεις επιπέδου Αρχιμήδη Νέων αλλά και Μεγάλων (όποιος όμως βάζει θέματα θα παρακαλούνταν να γράφει αν είναι για Νέους ή Μεγάλους) με σκοπό την προετοιμασία των παιδιών (συμπεριλαμβανομένου κι εμένα) για το συγκεκριμένο διαγωνισμό.
Ευχαριστώ.
Ευχαριστώ.
Προδρομίδης Κυπριανός-Ιάσων
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Αρχιμήδης 2014-2015
Καλησπέρα,
Υπάρχουν πολλά θέματα υψηλού ποιοτικού επιπέδου στους υποφακέλους seniors και juniors του φακέλου Μαθηματικοί Διαγωνισμοί και Ολυμπιάδες. Που μπορείς να προστρέξεις. Τα πιο έμπειρα μέλη του μπορούν να σε κατατοπίσουν καλύτερα.
μπορούν να σε κατατοπίσουν καλύτερα.
Με αφορμή όμως την ερώτηση σου, αν και είμαι νέο μέλος, αν μου επιτρέπετε να κάνω μια παρατήρηση.
Έχω παρατηρήσει συχνά στο φάκελο των juniors που από ότι γνωρίζω είναι για μαθητές μέχρι 15,5 χρονών
δηλαδή Γυμνάσιο ή Α' λυκείου για κάποιους που έχουν ξεκινήσει το σχολείο νωρίτερα. Υπάρχουν θέματα που ξεφεύγουν πολύ από αυτές τις ηλικίες και στην ύλη και στο σκοπό πιστεύω. Ειδικά σε φακέλους όπως εισαγωγή στα διαγνωστικά μαθηματικά για γυμνάσιο υπάρχουν θέματα μόνο εισαγωγή δεν είναι. Επειδή οι φάκελοι αυτοί θα πρέπει πρωταρχικά να απευθύνονται σε μαθητές ίσως θα πρέπει να είναι πιο αυστηρή η θεματολογία ειδικά για το Γυμνάσιο. Ώστε να ελκύουν το ενδιαφέρον του μαθητή παρά να τον αποτρέπουν με την δυσκολία.
Σαν μια πρόταση, δεν ξέρω αν είναι τεχνικά εφικτό, θα μπορούσε ίσως να υπάρχει μια επιλογή κλίμακας δυσκολίας (π.χ. από 1 έως 10) όπου ο κάθε θεματοδότης να αναρτά και το βαθμό δυσκολίας ή αν δε το γνωρίζει κάποιο πιο έμπειρο μέλος να το βαθμολογεί. Έτσι ίσως βοηθηθούν οι μαθητές πιο πολύ στην εισαγωγή τους στα διαγνωστικά μαθηματικά.
Θα επανέρθω αργότερα με την ανάρτηση μερικών θεμάτων αντίστοιχων διαγωνισμών, κυρίως από την Ρωσία.
Φιλικά,
Αλέξανδρος
Υπάρχουν πολλά θέματα υψηλού ποιοτικού επιπέδου στους υποφακέλους seniors και juniors του φακέλου Μαθηματικοί Διαγωνισμοί και Ολυμπιάδες. Που μπορείς να προστρέξεις. Τα πιο έμπειρα μέλη του
Με αφορμή όμως την ερώτηση σου, αν και είμαι νέο μέλος, αν μου επιτρέπετε να κάνω μια παρατήρηση.
Έχω παρατηρήσει συχνά στο φάκελο των juniors που από ότι γνωρίζω είναι για μαθητές μέχρι 15,5 χρονών
δηλαδή Γυμνάσιο ή Α' λυκείου για κάποιους που έχουν ξεκινήσει το σχολείο νωρίτερα. Υπάρχουν θέματα που ξεφεύγουν πολύ από αυτές τις ηλικίες και στην ύλη και στο σκοπό πιστεύω. Ειδικά σε φακέλους όπως εισαγωγή στα διαγνωστικά μαθηματικά για γυμνάσιο υπάρχουν θέματα μόνο εισαγωγή δεν είναι. Επειδή οι φάκελοι αυτοί θα πρέπει πρωταρχικά να απευθύνονται σε μαθητές ίσως θα πρέπει να είναι πιο αυστηρή η θεματολογία ειδικά για το Γυμνάσιο. Ώστε να ελκύουν το ενδιαφέρον του μαθητή παρά να τον αποτρέπουν με την δυσκολία.
Σαν μια πρόταση, δεν ξέρω αν είναι τεχνικά εφικτό, θα μπορούσε ίσως να υπάρχει μια επιλογή κλίμακας δυσκολίας (π.χ. από 1 έως 10) όπου ο κάθε θεματοδότης να αναρτά και το βαθμό δυσκολίας ή αν δε το γνωρίζει κάποιο πιο έμπειρο μέλος να το βαθμολογεί. Έτσι ίσως βοηθηθούν οι μαθητές πιο πολύ στην εισαγωγή τους στα διαγνωστικά μαθηματικά.
Θα επανέρθω αργότερα με την ανάρτηση μερικών θεμάτων αντίστοιχων διαγωνισμών, κυρίως από την Ρωσία.
Φιλικά,
Αλέξανδρος
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Αρχιμήδης 2014-2015
Σε διαγωνισμό στη πόλη Σαμάρα της Ρωσίας (το 2012) είχαν προταθεί τα παρακάτω θέματα μεταξύ άλλων.
1. Για την 9η τάξη (Γ' Γυνασιου - Α' Λυκείου)
Να βρεθεί η μέγιστη τιμή της παράστασης για
για 
2. Για την 10η τάξη (Α' Λυκείου -Β' Λυκείου)
Να βρεθεί η μέγιστη τιμή της παράστασης για
για 
3. Για την 11η τάξη (Β' Λυκείου - Γ' Λυκείου)
viewtopic.php?f=111&t=48093
1. Για την 9η τάξη (Γ' Γυνασιου - Α' Λυκείου)
Να βρεθεί η μέγιστη τιμή της παράστασης
 για
για 
2. Για την 10η τάξη (Α' Λυκείου -Β' Λυκείου)
Να βρεθεί η μέγιστη τιμή της παράστασης
 για
για 
3. Για την 11η τάξη (Β' Λυκείου - Γ' Λυκείου)
viewtopic.php?f=111&t=48093
Re: Αρχιμήδης 2014-2015
Ας λύσουμε το γενικό πρόβλημα:
Θέλουμε το μέγιστο της παράστασης για
για 
Έχουμε ότι
όπου χρησιμοποιήσαμε ότι (από ΑΜ-ΓΜ)
Θέλουμε το μέγιστο της παράστασης
 για
για 
Έχουμε ότι

όπου χρησιμοποιήσαμε ότι (από ΑΜ-ΓΜ)

Σιλουανός Μπραζιτίκος
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
Re: Αρχιμήδης 2014-2015
Άλλη μια καλή πιστεύω ανισότητα για μικρούς.
Έστω θετικοί πραγματικοί αριθμοί με
θετικοί πραγματικοί αριθμοί με  .Να αποδειχθεί ότι
.Να αποδειχθεί ότι

Έστω
 θετικοί πραγματικοί αριθμοί με
θετικοί πραγματικοί αριθμοί με  .Να αποδειχθεί ότι
.Να αποδειχθεί ότι 
Σημαντήρης Γιάννης
- G.Bas
- Δημοσιεύσεις: 705
- Εγγραφή: Τετ Οκτ 13, 2010 9:27 pm
- Τοποθεσία: Karditsa - Ioannina
- Επικοινωνία:
Re: Αρχιμήδης 2014-2015
Μετά τον μετασχηματισμόsimantiris j. έγραψε:Άλλη μια καλή πιστεύω ανισότητα για μικρούς.
Έστωθετικοί πραγματικοί αριθμοί με
.Να αποδειχθεί ότι
 η προς απόδειξη Ανισότητα ισοδύναμα γράφεται
η προς απόδειξη Ανισότητα ισοδύναμα γράφεται Σύμφωνα όμως με την Ανισότητα AM-GM θα ισχύει
Σύμφωνα όμως με την Ανισότητα AM-GM θα ισχύει
Μένει λοιπόν να αποδείξουμε την
 η οποία βέβαια είναι άμεση συνέπεια της Ανισότητας AM-GM.
η οποία βέβαια είναι άμεση συνέπεια της Ανισότητας AM-GM.Let Solutions Say Your Method!
George Basdekis
Cauchy-Schwarz is the best tool!
George Basdekis
Cauchy-Schwarz is the best tool!
-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Re: Αρχιμήδης 2014-2015
Και μια λύση και από εμένα, κατά τη γνώμη μου πιο απλή.simantiris j. έγραψε:Άλλη μια καλή πιστεύω ανισότητα για μικρούς.
Έστωθετικοί πραγματικοί αριθμοί με
.Να αποδειχθεί ότι
Από ΑΜ-ΓΜ και με βάση τη δοσμένη συνθήκη, έχουμε
 άρα αρκεί να αποδειχτεί ότι
άρα αρκεί να αποδειχτεί ότι ,
, που ισχύει.
Προδρομίδης Κυπριανός-Ιάσων
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Αρχιμήδης 2014-2015
ΑΣΚΗΣΗ 5(Για Junior)
Δίνεται τρίγωνο με περίκεντρο
με περίκεντρο  . Ο κύκλος που διέρχεται από τα σημεία
. Ο κύκλος που διέρχεται από τα σημεία  και εφάπτεται με την
και εφάπτεται με την  τέμνει τον κύκλο
τέμνει τον κύκλο  στο σημείο
στο σημείο  .
.
a) Να αποδειχθεί ότι
Συμπληρωματικό ερώτημα (για Senior) :
b) Αν η ευθεία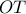 τέμνει την
τέμνει την  στο
στο  , να αποδειχθεί ότι η
, να αποδειχθεί ότι η  εφάπτεται με τον κύκλο
εφάπτεται με τον κύκλο 
Μπάμπης
Δίνεται τρίγωνο
 με περίκεντρο
με περίκεντρο  . Ο κύκλος που διέρχεται από τα σημεία
. Ο κύκλος που διέρχεται από τα σημεία  και εφάπτεται με την
και εφάπτεται με την  τέμνει τον κύκλο
τέμνει τον κύκλο  στο σημείο
στο σημείο  .
.a) Να αποδειχθεί ότι

Συμπληρωματικό ερώτημα (για Senior) :
b) Αν η ευθεία
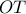 τέμνει την
τέμνει την  στο
στο  , να αποδειχθεί ότι η
, να αποδειχθεί ότι η  εφάπτεται με τον κύκλο
εφάπτεται με τον κύκλο 
Μπάμπης
Re: Αρχιμήδης 2014-2015
Γεια σας κύριε Μπάμπη.
Α) Θεωρούμε το μέσο της
της  .Το θεώρημα χορδής-εφαπτομένης δίνει
.Το θεώρημα χορδής-εφαπτομένης δίνει  .
.
Επίσης .Απ' τα προηγούμενα παίρνουμε
.Απ' τα προηγούμενα παίρνουμε  .
.
Επομένως το τετράπλευρο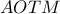 είναι εγγράψιμο απ' όπου παίρνουμε
είναι εγγράψιμο απ' όπου παίρνουμε  όπως θέλαμε.
όπως θέλαμε.

Β)Τα κέντρα των κύκλων και
και  είναι συνευθειακά άρα αυτοί είναι εφαπτόμενοι εσωτερικά.
είναι συνευθειακά άρα αυτοί είναι εφαπτόμενοι εσωτερικά.
Η ευθεία είναι ριζικός άξονας των κύκλων
είναι ριζικός άξονας των κύκλων  και
και  .Η ευθεία
.Η ευθεία  είναι ριζικός άξονας των κύκλων
είναι ριζικός άξονας των κύκλων  και
και  .
.
Άρα το είναι το ριζικό κέντρο των τριών κύκλων του σχήματος.Επομένως ο ριζικός άξονας των κύκλων
είναι το ριζικό κέντρο των τριών κύκλων του σχήματος.Επομένως ο ριζικός άξονας των κύκλων  και
και  περνά από αυτό.
περνά από αυτό.
Όμως ριζικός άξονας δύο εσωτερικά εφαπτόμενων κύκλων είναι η κοινή εξωτερική τους εφαπτομένη.Άρα η εφάπτεται στους δύο κύκλους που είναι το ζητούμενο.
εφάπτεται στους δύο κύκλους που είναι το ζητούμενο.
Α) Θεωρούμε το μέσο
 της
της  .Το θεώρημα χορδής-εφαπτομένης δίνει
.Το θεώρημα χορδής-εφαπτομένης δίνει  .
.Επίσης
 .Απ' τα προηγούμενα παίρνουμε
.Απ' τα προηγούμενα παίρνουμε  .
.Επομένως το τετράπλευρο
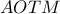 είναι εγγράψιμο απ' όπου παίρνουμε
είναι εγγράψιμο απ' όπου παίρνουμε  όπως θέλαμε.
όπως θέλαμε.
Β)Τα κέντρα των κύκλων
 και
και  είναι συνευθειακά άρα αυτοί είναι εφαπτόμενοι εσωτερικά.
είναι συνευθειακά άρα αυτοί είναι εφαπτόμενοι εσωτερικά.Η ευθεία
 είναι ριζικός άξονας των κύκλων
είναι ριζικός άξονας των κύκλων  και
και  .Η ευθεία
.Η ευθεία  είναι ριζικός άξονας των κύκλων
είναι ριζικός άξονας των κύκλων  και
και  .
.Άρα το
 είναι το ριζικό κέντρο των τριών κύκλων του σχήματος.Επομένως ο ριζικός άξονας των κύκλων
είναι το ριζικό κέντρο των τριών κύκλων του σχήματος.Επομένως ο ριζικός άξονας των κύκλων  και
και  περνά από αυτό.
περνά από αυτό.Όμως ριζικός άξονας δύο εσωτερικά εφαπτόμενων κύκλων είναι η κοινή εξωτερική τους εφαπτομένη.Άρα η
 εφάπτεται στους δύο κύκλους που είναι το ζητούμενο.
εφάπτεται στους δύο κύκλους που είναι το ζητούμενο.Γιώργος Γαβριλόπουλος
-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Re: Αρχιμήδης 2014-2015
Άσκηση 6 (Juniors)
Έστω τρίγωνο εγγεγραμμένο σε κύκλο. Το ύψος του
εγγεγραμμένο σε κύκλο. Το ύψος του 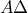 τέμνει τον περιγεγραμμένο κύκλο του τριγώνου στο
τέμνει τον περιγεγραμμένο κύκλο του τριγώνου στο  , και ο περιγεγραμμένος κύκλος του
, και ο περιγεγραμμένος κύκλος του  τέμνει την
τέμνει την  στο
στο  . Επίσης, αν η
. Επίσης, αν η  τέμνει την
τέμνει την  στο
στο  και η
και η  τέμνει την
τέμνει την  στο
στο 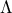 , να αποδείξετε ότι το
, να αποδείξετε ότι το  είναι το μέσο της
είναι το μέσο της  .
.
Έστω τρίγωνο
 εγγεγραμμένο σε κύκλο. Το ύψος του
εγγεγραμμένο σε κύκλο. Το ύψος του 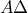 τέμνει τον περιγεγραμμένο κύκλο του τριγώνου στο
τέμνει τον περιγεγραμμένο κύκλο του τριγώνου στο  , και ο περιγεγραμμένος κύκλος του
, και ο περιγεγραμμένος κύκλος του  τέμνει την
τέμνει την  στο
στο  . Επίσης, αν η
. Επίσης, αν η  τέμνει την
τέμνει την  στο
στο  και η
και η  τέμνει την
τέμνει την  στο
στο 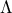 , να αποδείξετε ότι το
, να αποδείξετε ότι το  είναι το μέσο της
είναι το μέσο της  .
.
τελευταία επεξεργασία από Φωτεινή σε Δευ Φεβ 09, 2015 10:27 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λόγος: $LaTeX$
Λόγος: $LaTeX$
Προδρομίδης Κυπριανός-Ιάσων
Re: Αρχιμήδης 2014-2015
Καλησπέρα.jasonmaths4ever έγραψε:Άσκηση 6 (Juniors)
Έστω τρίγωνο ΑΒΓ εγγεγραμμένο σε κύκλο. Το ύψος του ΑΔ τέμνει τον περιγεγραμμένο κύκλο του τριγώνου στο Ζ, και ο περιγεγραμμένος κύκλος του ΒΔΖ τέμνει την ΑΒ στο Ε. Επίσης, αν η ΔΕ τέμνει την ΑΓ στο Κ και η ΖΚ τέμνει την ΒΓ στο Λ, να αποδείξετε ότι το Δ είναι το μέσο της ΒΛ.
Έστω
 η προβολή του
η προβολή του  στην
στην  .Από το εγγεγραμμένο
.Από το εγγεγραμμένο  παίρνουμε
παίρνουμε  .
.Επομένως η ευθεία
 είναι η ευθεία Simson του σημείου
είναι η ευθεία Simson του σημείου  ως προς το τρίγωνο
ως προς το τρίγωνο  .
.Άρα
 .Επειδή το σημείο τομής των
.Επειδή το σημείο τομής των  είναι μοναδικό ισχύει
είναι μοναδικό ισχύει  .
.Επομένως
 δηλαδή το
δηλαδή το  είναι εγγράψιμο.
είναι εγγράψιμο.Επομένως
 δηλαδή στο τρίγωνο
δηλαδή στο τρίγωνο  η
η  είναι ύψος και διχοτόμος δηλαδή αυτό είναι ισοσκελές και το ζητούμενο έπεται.
είναι ύψος και διχοτόμος δηλαδή αυτό είναι ισοσκελές και το ζητούμενο έπεται.Γιώργος Γαβριλόπουλος
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Αρχιμήδης 2014-2015
Άσκηση 7 (Juniors)
Ο Πέτρος θέλει να γράψει όλες τις ακολουθίες 100 φυσικών αριθμών στην καθε μία από τις οποίες εμφανίζεται τουλάχιστον μία φορά το 3 και οποιηδήποτε δυο διαδοχικοί όροι δεν διαφέρουν περισσότερο από 1. Πόσες ακολουθίες θα πρέπει να γράψει;
Ο Πέτρος θέλει να γράψει όλες τις ακολουθίες 100 φυσικών αριθμών στην καθε μία από τις οποίες εμφανίζεται τουλάχιστον μία φορά το 3 και οποιηδήποτε δυο διαδοχικοί όροι δεν διαφέρουν περισσότερο από 1. Πόσες ακολουθίες θα πρέπει να γράψει;
τελευταία επεξεργασία από Al.Koutsouridis σε Τρί Φεβ 10, 2015 1:17 am, έχει επεξεργασθεί 2 φορές συνολικά.
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Αρχιμήδης 2014-2015
Συμφωνώ Αλέξανδρε με την πρότασή σου , (για το θέμα "ΕΙΣΑΓΩΓΗ ΣΕ ΔΙΑΓΩΝΙΣΤΙΚΑ ΜΑΘΗΜΑΤΙΚΑ - ΓΥΜΝΑΣΙΟ"), όπου παρά το γεγονός ότι ο βαθμός δυσκολίας είναι πολλές φορές υποκειμενικός, σίγουρα βοηθάει αυτόν που θέλει να ασχοληθεί με κάποια άσκηση . Προσωπικά, σε όσεςAl.Koutsouridis έγραψε:Καλησπέρα,
Σαν μια πρόταση, δεν ξέρω αν είναι τεχνικά εφικτό, θα μπορούσε ίσως να υπάρχει μια επιλογή κλίμακας δυσκολίας (π.χ. από 1 έως 10) όπου ο κάθε θεματοδότης να αναρτά και το βαθμό δυσκολίας ή αν δε το γνωρίζει κάποιο πιο έμπειρο μέλος να το βαθμολογεί. Έτσι ίσως βοηθηθούν οι μαθητές πιο πολύ στην εισαγωγή τους στα διαγνωστικά μαθηματικά.
Φιλικά,
Αλέξανδρος
αναρτώ στο εξής, θα γράφω δίπλα και τον βαθμό δυσκολίας (με την κλίμακα από 1 έως 10)
-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Re: Αρχιμήδης 2014-2015
(Υποθέτω ότι οι ακολουθίες είναι αύξουσες και δίνω μια λύση, χωρίς να είμαι απόλυτα σίγουρος)Al.Koutsouridis έγραψε:Άσκηση 7 (Juniors)
Ο Πέτρος θέλει να γράψει όλες τις ακολουθίες 100 φυσικών αριθμών στην καθε μία από τις οποίες εμφανίζεται τουλάχιστον μία φορά το 3 και οποιηδήποτε δυο διαδοχικοί όροι δεν διαφέρουν περισσότερο από 1. Πόσες ακολουθίες θα πρέπει να γράψει;
Σταθεροποιούμε τον πρώτο όρο της ακολουθίας, ο οποίος παίρνει μία από τις τιμές 0,1,2,3. Η διαφορά δύο διαδοχικών όρων παίρνει τις τιμές 0,1, από υπόθεση. Συνολικά έχουμε 99 διαφορές μεταξύ δύο διαδοχικών όρων. Αν ο πρώτος όρος της ακολουθίας είναι ο 3, τότε η διαφορά δύο διαδοχικών όρων μπορεί να επιλεγεί με 2 τρόπους (0,1). Άρα έχουμε συνολικά
 ακολουθίες με πρώτο όρο το 3. Αν ο πρώτος όρος της ακολουθίας είναι το 2, τότε έχουμε πάλι
ακολουθίες με πρώτο όρο το 3. Αν ο πρώτος όρος της ακολουθίας είναι το 2, τότε έχουμε πάλι  μόνο που πρέπει να αφαιρέσουμε την ακολουθία 2,2,2,...,2 αφού δεν περιέχει το 3 μέσα. Άρα συνολικά έχουμε
μόνο που πρέπει να αφαιρέσουμε την ακολουθία 2,2,2,...,2 αφού δεν περιέχει το 3 μέσα. Άρα συνολικά έχουμε  ακολουθίες με πρώτο όρο το 2. Αν ο πρώτος όρος της ακολουθίας είναι το 1, τότε πάλι αφαιρούμε την ακολουθία που έχει μόνο 1, αλλά και τις ακολουθίες που έχουν μόνο άσσους και δυάρια (σε πλήθος 99). Άρα σύνολο
ακολουθίες με πρώτο όρο το 2. Αν ο πρώτος όρος της ακολουθίας είναι το 1, τότε πάλι αφαιρούμε την ακολουθία που έχει μόνο 1, αλλά και τις ακολουθίες που έχουν μόνο άσσους και δυάρια (σε πλήθος 99). Άρα σύνολο  ακολουθίες με πρώτο όρο το 1. Τέλος, με πρώτο όρο το 0 έχουμε πάλι
ακολουθίες με πρώτο όρο το 1. Τέλος, με πρώτο όρο το 0 έχουμε πάλι  ακολουθίες, όμως τώρα πρέπει να αφαιρέσουμε όλες εκείνες τις ακολουθίες που έχουν: μόνο 0(1 σε πλήθος), μόνο 0 και 1(99 σε πλήθος) αλλά και αυτές που έχουν μόνο 0,1,2(99*98 σε πλήθος). Άρα συνολικά έχουμε
ακολουθίες, όμως τώρα πρέπει να αφαιρέσουμε όλες εκείνες τις ακολουθίες που έχουν: μόνο 0(1 σε πλήθος), μόνο 0 και 1(99 σε πλήθος) αλλά και αυτές που έχουν μόνο 0,1,2(99*98 σε πλήθος). Άρα συνολικά έχουμε  ακολουθίες.
ακολουθίες. .
Προδρομίδης Κυπριανός-Ιάσων
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Αρχιμήδης 2014-2015
Δεν αναφέρεται ρητά ούτε στην εκφώνηση από την πηγή που το πήρα αλλά νομίζω θα πρέπει να θεωρήσουμε φυσικούς το σύνολοjasonmaths4ever έγραψε:
(Υποθέτω ότι οι ακολουθίες είναι αύξουσες και δίνω μια λύση, χωρίς να είμαι απόλυτα σίγουρος)
Σταθεροποιούμε τον πρώτο όρο της ακολουθίας, ο οποίος παίρνει μία από τις τιμές 0,1,2,3. .

και να μην περιοριστούμε μόνο στις αύξουσες ακολουθίες.
-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Re: Αρχιμήδης 2014-2015
Είσαι σίγουρος τότε ότι το επίπεδο είναι για μικρούς; Εγώ το βρίσκω πολύ δύσκολο πρόβλημα...Al.Koutsouridis έγραψε:Και να μην περιοριστούμε μόνο στις αύξουσες ακολουθίες.jasonmaths4ever έγραψε:
(Υποθέτω ότι οι ακολουθίες είναι αύξουσες και δίνω μια λύση, χωρίς να είμαι απόλυτα σίγουρος)
Σταθεροποιούμε τον πρώτο όρο της ακολουθίας, ο οποίος παίρνει μία από τις τιμές 0,1,2,3. .
Προδρομίδης Κυπριανός-Ιάσων
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Αρχιμήδης 2014-2015
Και εμένα μου έκανε εντύπωση η δυσκολία για αυτό και το βρήκα ενδιαφέρων και το πρότεινα, αλλά ναι είναι θέμα της 9ης τάξης.
τελευταία επεξεργασία από Al.Koutsouridis σε Τρί Φεβ 10, 2015 5:36 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Αρχιμήδης 2014-2015
Άσκηση 8 (Κάνει και για Seniors και για Juniors)
Δίνονται διακεκριμένα σημεία στο επίπεδο. Χρωματίζουμε κόκκινα τα μέσα όλων των ευθυγράμμων τμημάτων που ορίζονται από αυτά τα σημεία. Να βρεθεί ο ελάχιστος δυνατός αριθμός διαφορετικών κόκκινων σημείων.
διακεκριμένα σημεία στο επίπεδο. Χρωματίζουμε κόκκινα τα μέσα όλων των ευθυγράμμων τμημάτων που ορίζονται από αυτά τα σημεία. Να βρεθεί ο ελάχιστος δυνατός αριθμός διαφορετικών κόκκινων σημείων.
Δίνονται
 διακεκριμένα σημεία στο επίπεδο. Χρωματίζουμε κόκκινα τα μέσα όλων των ευθυγράμμων τμημάτων που ορίζονται από αυτά τα σημεία. Να βρεθεί ο ελάχιστος δυνατός αριθμός διαφορετικών κόκκινων σημείων.
διακεκριμένα σημεία στο επίπεδο. Χρωματίζουμε κόκκινα τα μέσα όλων των ευθυγράμμων τμημάτων που ορίζονται από αυτά τα σημεία. Να βρεθεί ο ελάχιστος δυνατός αριθμός διαφορετικών κόκκινων σημείων.-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Αρχιμήδης 2014-2015
Άσκηση 9
2015 στρατιώτες είναι τοποθετημένοι στο πεδίο της μάχης έτσι ώστε όλα τα δυνατά ζεύγη να αντιστοιχούν σε διαφορετικές αποστάσεις. Κάθε στρατιώτης καλύπτει τον στρατιώτη που βρίσκεται πιο κοντά του. Αποδείξτε ότι τουλάχιστον ένας στρατιώτης θα μείνει ακάλυπτος.
2015 στρατιώτες είναι τοποθετημένοι στο πεδίο της μάχης έτσι ώστε όλα τα δυνατά ζεύγη να αντιστοιχούν σε διαφορετικές αποστάσεις. Κάθε στρατιώτης καλύπτει τον στρατιώτη που βρίσκεται πιο κοντά του. Αποδείξτε ότι τουλάχιστον ένας στρατιώτης θα μείνει ακάλυπτος.
Θανάσης Κοντογεώργης
Re: Αρχιμήδης 2014-2015
Καλημέρα σε όλους! Ευχαριστούμε για τις όμορφες ασκήσεις! Μία σκέψη:socrates έγραψε:Άσκηση 9
2015 στρατιώτες είναι τοποθετημένοι στο πεδίο της μάχης έτσι ώστε όλα τα δυνατά ζεύγη να αντιστοιχούν σε διαφορετικές αποστάσεις. Κάθε στρατιώτης καλύπτει τον στρατιώτη που βρίσκεται πιο κοντά του. Αποδείξτε ότι τουλάχιστον ένας στρατιώτης θα μείνει ακάλυπτος.
Αφού όλοι έχουν διαφορετικές αποστάσεις, υπάρχουν
 , έστω ο
, έστω ο  και ο
και ο  με την ελάχιστη απόσταση. Τότε ο
με την ελάχιστη απόσταση. Τότε ο  καλύπτει τον
καλύπτει τον  και ο
και ο  τον
τον  .
.Από τους υπόλοιπους
 αν κάποιος έχει ως κοντινότερο τον
αν κάποιος έχει ως κοντινότερο τον  ή τον
ή τον  κάποιος προφανώς θα μείνει ακάλυπτος. Διαφορετικά υπάρχουν πάλι
κάποιος προφανώς θα μείνει ακάλυπτος. Διαφορετικά υπάρχουν πάλι  με την ελάχιστη απόσταση.
με την ελάχιστη απόσταση.Συνεχίζοντας τη διαδικασία θα φτάσουμε σε
 άτομα για τα οποία αν
άτομα για τα οποία αν  είναι οι στρατιώτες με την ελάχιστη απόσταση τότε αναγκαστικά το τρίτο άτομο θα μείνει ακάλυπτο.
είναι οι στρατιώτες με την ελάχιστη απόσταση τότε αναγκαστικά το τρίτο άτομο θα μείνει ακάλυπτο.
τελευταία επεξεργασία από raf616 σε Τετ Φεβ 11, 2015 1:57 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Πάντα κατ' αριθμόν γίγνονται... ~ Πυθαγόρας
Ψυρούκης Ραφαήλ
Ψυρούκης Ραφαήλ
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
