
IMC 2015/2/1
Συντονιστής: Demetres
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: IMC 2015/2/1
ΈστωDemetres έγραψε:Να δειχθεί ότι
 το ζητούμενο άθροισμα τότε:
το ζητούμενο άθροισμα τότε:![\displaystyle{\begin{aligned}
S=\sum_{n=1}^{\infty}\frac{1}{\sqrt{n}\left ( n+1 \right )}&= \sum_{n=1}^{\infty}\frac{\sqrt{n}}{n(n+1)} \\
&=\sum_{n=1}^{\infty}\left [ \frac{\sqrt{n}}{n}- \frac{\sqrt{n}}{n+1} \right ]\\
&= \frac{\sqrt{1}}{1}+ \sum_{n=1}^{\infty} \left[ \frac{\sqrt{n+1}}{n+1}-\frac{\sqrt{n}}{n+1} \right]\\
&=1+ \sum_{n=1}^{\infty}\frac{1}{\left ( n+1 \right )\left ( \sqrt{n}+\sqrt{n+1} \right )} \\
&\overset{CS}{\leq} 1+ \frac{1}{4}\sum_{n=1}^{\infty}\left [ \frac{1}{\sqrt{n+1}(n+1)} + \frac{1}{\sqrt{n}(n+1)} \right ]\\
&= 1+ \frac{S}{4}+ \frac{1}{4}\sum_{n=2}^{\infty}\frac{1}{n^{3/2}}
\end{aligned}} \displaystyle{\begin{aligned}
S=\sum_{n=1}^{\infty}\frac{1}{\sqrt{n}\left ( n+1 \right )}&= \sum_{n=1}^{\infty}\frac{\sqrt{n}}{n(n+1)} \\
&=\sum_{n=1}^{\infty}\left [ \frac{\sqrt{n}}{n}- \frac{\sqrt{n}}{n+1} \right ]\\
&= \frac{\sqrt{1}}{1}+ \sum_{n=1}^{\infty} \left[ \frac{\sqrt{n+1}}{n+1}-\frac{\sqrt{n}}{n+1} \right]\\
&=1+ \sum_{n=1}^{\infty}\frac{1}{\left ( n+1 \right )\left ( \sqrt{n}+\sqrt{n+1} \right )} \\
&\overset{CS}{\leq} 1+ \frac{1}{4}\sum_{n=1}^{\infty}\left [ \frac{1}{\sqrt{n+1}(n+1)} + \frac{1}{\sqrt{n}(n+1)} \right ]\\
&= 1+ \frac{S}{4}+ \frac{1}{4}\sum_{n=2}^{\infty}\frac{1}{n^{3/2}}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/cef95c33237a359c8daf0e51fca7e6a4.png)
Για το τελευταίο άθροισμα χρησιμοποιούμε την εκτίμηση του ολοκλήρωματος και έχουμε ότι:

και το συμπέρασμα έπεται αφού
 . Για την ακρίβεια , χρησιμοποιώντας τη τεχνολογία, βλέπουμε ότι η σειρά είναι περίπου
. Για την ακρίβεια , χρησιμοποιώντας τη τεχνολογία, βλέπουμε ότι η σειρά είναι περίπου  .
.Η φαντασία είναι σημαντικότερη από τη γνώση !


-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: IMC 2015/2/1
Γεια σας. Ωραίες οι λύσεις.
Με το ολοκληρωτικό κριτήριο του μπορούμε να βρούμε και ένα κάτω φράγμα για τη σειρά.
μπορούμε να βρούμε και ένα κάτω φράγμα για τη σειρά.
Ορίζουμε με τύπο
με τύπο  .
.
Η συνάρτηση είναι συνεχής, θετική και γνησίως φθίνουσα στο
είναι συνεχής, θετική και γνησίως φθίνουσα στο  με
με
 . Έχουμε ότι
. Έχουμε ότι
![\displaystyle{\begin{aligned} \int_{1}^{+\infty}f(x)\,\mathrm{d}x&=\int_{1}^{\infty}\dfrac{1}{\sqrt{x}\,(x+1)}\,\mathrm{d}x\\&\stackrel{y=\sqrt{x}}{=}\int_{1}^{+\infty}\dfrac{2}{1+y^2}\,\mathrm{d}y\\&=\left[2\,\arctan\,y\right]_{1}^{+\infty}\\&=\pi-\dfrac{\pi}{2}\\&=\dfrac{\pi}{2}\end{aligned}} \displaystyle{\begin{aligned} \int_{1}^{+\infty}f(x)\,\mathrm{d}x&=\int_{1}^{\infty}\dfrac{1}{\sqrt{x}\,(x+1)}\,\mathrm{d}x\\&\stackrel{y=\sqrt{x}}{=}\int_{1}^{+\infty}\dfrac{2}{1+y^2}\,\mathrm{d}y\\&=\left[2\,\arctan\,y\right]_{1}^{+\infty}\\&=\pi-\dfrac{\pi}{2}\\&=\dfrac{\pi}{2}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/4f60a84669584fc231dd1cbecefb7b39.png)
Σύμφωνα με το κριτήριο του , η πραγματική ακολουθία
, η πραγματική ακολουθία 
συγκλίνει προς κάποιο στοιχείο του![\displaystyle{\left[0,f(1)\right]=\left[0,\dfrac{1}{2}\right]} \displaystyle{\left[0,f(1)\right]=\left[0,\dfrac{1}{2}\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/9a94a5807dce212426cf19927e55e40e.png) , οπότε :
, οπότε :
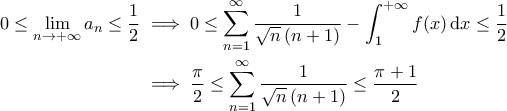
Συμπεραίνουμε ότι .
.
Με το ολοκληρωτικό κριτήριο του
 μπορούμε να βρούμε και ένα κάτω φράγμα για τη σειρά.
μπορούμε να βρούμε και ένα κάτω φράγμα για τη σειρά.Ορίζουμε
 με τύπο
με τύπο  .
.Η συνάρτηση
 είναι συνεχής, θετική και γνησίως φθίνουσα στο
είναι συνεχής, θετική και γνησίως φθίνουσα στο  με
με . Έχουμε ότι
. Έχουμε ότι![\displaystyle{\begin{aligned} \int_{1}^{+\infty}f(x)\,\mathrm{d}x&=\int_{1}^{\infty}\dfrac{1}{\sqrt{x}\,(x+1)}\,\mathrm{d}x\\&\stackrel{y=\sqrt{x}}{=}\int_{1}^{+\infty}\dfrac{2}{1+y^2}\,\mathrm{d}y\\&=\left[2\,\arctan\,y\right]_{1}^{+\infty}\\&=\pi-\dfrac{\pi}{2}\\&=\dfrac{\pi}{2}\end{aligned}} \displaystyle{\begin{aligned} \int_{1}^{+\infty}f(x)\,\mathrm{d}x&=\int_{1}^{\infty}\dfrac{1}{\sqrt{x}\,(x+1)}\,\mathrm{d}x\\&\stackrel{y=\sqrt{x}}{=}\int_{1}^{+\infty}\dfrac{2}{1+y^2}\,\mathrm{d}y\\&=\left[2\,\arctan\,y\right]_{1}^{+\infty}\\&=\pi-\dfrac{\pi}{2}\\&=\dfrac{\pi}{2}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/4f60a84669584fc231dd1cbecefb7b39.png)
Σύμφωνα με το κριτήριο του
 , η πραγματική ακολουθία
, η πραγματική ακολουθία 
συγκλίνει προς κάποιο στοιχείο του
![\displaystyle{\left[0,f(1)\right]=\left[0,\dfrac{1}{2}\right]} \displaystyle{\left[0,f(1)\right]=\left[0,\dfrac{1}{2}\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/9a94a5807dce212426cf19927e55e40e.png) , οπότε :
, οπότε :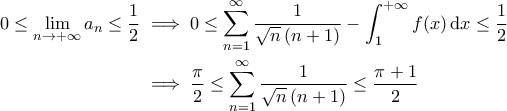
Συμπεραίνουμε ότι
 .
.Παπαπέτρος Ευάγγελος
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: IMC 2015/2/1
Βαγγέλη, ίσως δεν καταλαβαίνω κάτι.BAGGP93 έγραψε:Από τη σχέση αυτή έχουμε
![\displaystyle{\sum_{n=1}^{\infty}\dfrac{1}{\sqrt{n}\,(n+1)}\in\left[\dfrac{\pi}{2},\dfrac{\pi+1}{2}\right]} \displaystyle{\sum_{n=1}^{\infty}\dfrac{1}{\sqrt{n}\,(n+1)}\in\left[\dfrac{\pi}{2},\dfrac{\pi+1}{2}\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/973224cf6e1c5972fe0730c8540137a9.png)
άλλα όπως δείξαμε
άρα.
Όταν λες "όπως δείξαμε" εννοείς σε άλλη (ξένη) απόδειξη; Μη ξεχνάς ότι το
 είναι το ζητούμενο της άσκησης. Οπότε προς τι όλη η επιχειρηματολογία με κριτήριο Cauchy και ολοκληρώμα;
είναι το ζητούμενο της άσκησης. Οπότε προς τι όλη η επιχειρηματολογία με κριτήριο Cauchy και ολοκληρώμα; Μη ξεχνάς ότι
 οπότε δεν βλέπω πώς καταλήγουμε σε εκτίμηση ότι το άθροισμα είναι
οπότε δεν βλέπω πώς καταλήγουμε σε εκτίμηση ότι το άθροισμα είναι  .
.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες




