 με ακέραιους συντελεστές ώστε
με ακέραιους συντελεστές ώστε ![P(\sqrt[3]{5} + \sqrt[3]{25}) = 5+\sqrt[3]{5} P(\sqrt[3]{5} + \sqrt[3]{25}) = 5+\sqrt[3]{5}](/forum/ext/geomar/texintegr/latexrender/pictures/b8153481aa16ee271cd2b64ae46ad924.png) .
.Συντονιστής: Demetres
 με ακέραιους συντελεστές ώστε
με ακέραιους συντελεστές ώστε ![P(\sqrt[3]{5} + \sqrt[3]{25}) = 5+\sqrt[3]{5} P(\sqrt[3]{5} + \sqrt[3]{25}) = 5+\sqrt[3]{5}](/forum/ext/geomar/texintegr/latexrender/pictures/b8153481aa16ee271cd2b64ae46ad924.png) .
.![\alpha = \sqrt[3]{5} \alpha = \sqrt[3]{5}](/forum/ext/geomar/texintegr/latexrender/pictures/fc80874f0478a26583f0fe0f5463072a.png) και
και  . Επειδή
. Επειδή  και ο
και ο  έχει βαθμό
έχει βαθμό  , τότε ο βαθμός του
, τότε ο βαθμός του  διαιρεί το
διαιρεί το  . Δεν είναι δύσκολο να δειχθεί ότι ο βαθμός του
. Δεν είναι δύσκολο να δειχθεί ότι ο βαθμός του  δεν είναι
δεν είναι  αλλά μπορούμε πιο γρήγορα να παρατηρήσουμε ότι αν ο βαθμός ήταν
αλλά μπορούμε πιο γρήγορα να παρατηρήσουμε ότι αν ο βαθμός ήταν  , τότε το
, τότε το  θα ήταν ρητός, άτοπο.
θα ήταν ρητός, άτοπο.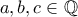 ώστε
ώστε  .
. είναι αλγεβρικοί ακέραιοι (ρίζες μονικών πολυωνύμων με ακέραιους συντελεστές) το ίδιο ισχύει και για τον
είναι αλγεβρικοί ακέραιοι (ρίζες μονικών πολυωνύμων με ακέραιους συντελεστές) το ίδιο ισχύει και για τον  . [Οι αλγεβρικοί ακέραιοι είναι δακτύλιος.] Οπότε οι
. [Οι αλγεβρικοί ακέραιοι είναι δακτύλιος.] Οπότε οι  που βρήκαμε πιο πάνω είναι ακέραιοι.
που βρήκαμε πιο πάνω είναι ακέραιοι.  . Οπότε
. Οπότε 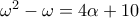 . Άρα
. Άρα 
 , άτοπο.
, άτοπο. τότε προφανώς
τότε προφανώς
 ,
,  ακέραιοι.
ακέραιοι. τότε
τότε  άρα
άρα 

 ακέραιος.
ακέραιος. δεν είναι μοναδικά. Δεν είμαι σίγουρος λοιπόν πως καταλήγεις σε άτοπο. Δεν θα μπορούσε π.χ. να είναι
δεν είναι μοναδικά. Δεν είμαι σίγουρος λοιπόν πως καταλήγεις σε άτοπο. Δεν θα μπορούσε π.χ. να είναι  και
και  ;
;
 θα έχει λύσεις
θα έχει λύσεις 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες